
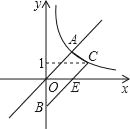
【题目】如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,﹣4),则四边形AOBC的面积为_____.
【答案】2![]() +10.
+10.
【解析】因为AO∥BC,上底边OA在直线y=x上,
则可设BC的解析式为y=x+b,
将B(0,﹣4)代入上式得,b=﹣4,
BC的解析式为y=x﹣4.
把y=1代入y=x﹣4,得x=5,C点坐标为(5,1),
则反比例函数解析式为y=![]() ,
,
将它与y=x组成方程组得:![]() ,
,
解得x=![]() ,x=﹣
,x=﹣![]() (负值舍去).
(负值舍去).
代入y=x得,y=![]() ,
,
A点坐标为(![]() ,
,![]() ),
),
OA=![]() =
=![]() ,
,
BC=![]() =5
=5![]() ,
,
∵BC的解析式为y=x﹣4,
∴E(4,0),
∵B(0,﹣4),
∴BE=![]() =4
=4![]() ,
,
设BE边上的高为h,
![]() h×
h×![]() =4×4×
=4×4×![]() ,
,
解得:h=2![]() ,
,
则梯形AOBC高为:2![]() ,
,
梯形AOBC面积为:![]() ×2
×2![]() ×(
×(![]() +5
+5![]() )=2
)=2![]() +10,
+10,
故答案为:2![]() +10.
+10.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】计算与化简
(1)-18+21+(-13)
(2)-81÷![]() ×
×![]() ÷(-16)
÷(-16)
(3)(![]() +
+![]() -
-![]() )×(-24)
)×(-24)
(4)-22-![]() ×[4-(-3)2]
×[4-(-3)2]
(5)化简:5(3x2y-xy2)-4(-xy2+2x2y)
(6)先化简,再求值:-![]() x+2(x-
x+2(x-![]() y2) - (-
y2) - (-![]() x+
x+![]() y2);其中x=2,y=
y2);其中x=2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1,AA2,AA3…,依此作法,则∠AAnAn+1等于______度.(用含n的代数式表示,n为正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手工拉面是我国的传统美食.已知1根面条拉扣1次成2根.拉扣2次就成2x2根……每拉扣1次,面条数就增加1倍.
(1)设2位师傅各拿1根面条分别拉扣3次所成面条数之和为![]() ,3位师傅各拿1根面条分别拉扣2次所成面条数之和为
,3位师傅各拿1根面条分别拉扣2次所成面条数之和为![]() .试通过计算比较
.试通过计算比较![]() 的大小;
的大小;
(2)设张师傅在某次拉扣后所成面条的长度为0.8米/根,总长度为![]() 米,如果他又拉扣了2次,求此时面条增加了多少根?
米,如果他又拉扣了2次,求此时面条增加了多少根?
查看答案和解析>>
科目:初中数学 来源: 题型:
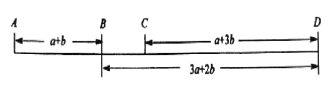
【题目】己知![]() 四个车站的位置如图所示.
四个车站的位置如图所示.
(1)求![]() 两站之间的距离;(用含
两站之间的距离;(用含![]() 的代数式表示)
的代数式表示)
(2)一辆汽车从![]() 站出发,每小时行驶60千米,经过
站出发,每小时行驶60千米,经过![]() 站到达C站(在
站到达C站(在![]() 站没有停留).所用时间为1.5小时.汽车在
站没有停留).所用时间为1.5小时.汽车在![]() 站短暂停留后,继续以相同速度行驶,再行驶2小时到达
站短暂停留后,继续以相同速度行驶,再行驶2小时到达![]() 站,求
站,求![]() 的值以及汽车从
的值以及汽车从![]() 站行驶到
站行驶到![]() 站一共用了多少小时?
站一共用了多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
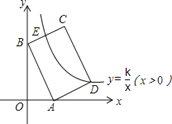
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=![]() (x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:圆是最完美的图形,它具有一些特殊的性质:同弧或等弧所对的圆周角相等,一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”,再利用圆的性质将问题进行转化,往往能化隐为显、化难为易。
解决问题:如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.
(1)使∠APB=30°的点P有_______个;
(2)若点P在y轴正半轴上,且∠APB=30°,求满足条件的点P的坐标;
(3)设sin∠APB=m,若点P在y轴上移动时, 满足条件的点P有4个,求m的取值范围.
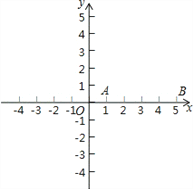
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个两位数A,十位数字为a,个位数字为b,交换a和b的位置,得到一个新的两位数B,则A+B一定能被______整除,A-B一定能被______整除;
(2)一个三位数M,百位数字为a,十位数字为b,个位数字为c(a,b,c均为1至9的整数),交换a和c的位置,得到一个新的三位数N.请用含a、b、c的式子分别表示数N与M-N;
(3) 若(2)中a比b大1,M比N大792,求M.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com