
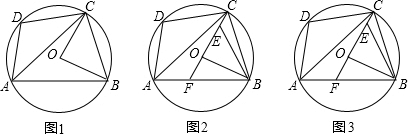
分析 (1)如图1中,连接OA,只要证明∠CAB=∠1+∠2=∠ACO+∠ABO,由点C是$\widehat{BD}$中点,推出$\widehat{CD}$=$\widehat{CB}$,推出∠BAC=∠DAC,即可推出∠DAC=∠ACO+∠ABO;
(2)想办法证明∠EFB=∠EBF即可;
(3)如图3中,过点O作OH⊥AB,垂足为H,延长BE交HO的延长线于G,作BN⊥CF于N,作CK⊥AD于K,连接OA.作CT∠⊥AB于T.首先证明△EFB是等边三角形,再证明△ACK≌△ACT,Rt△DKC≌Rt△BTC,延长即可解决问题;
解答 解:(1)如图1中,连接OA,
∵OA=OC,
∴∠1=∠ACO,
∵OA=OB,
∴∠2=∠ABO,
∴∠CAB=∠1+∠2=∠ACO+∠ABO,
∵点C是$\widehat{BD}$中点,
∴$\widehat{CD}$=$\widehat{CB}$,
∴∠BAC=∠DAC,
∴∠DAC=∠ACO+∠ABO.
(2)如图2中,
∵∠BAD=∠BAC+∠DAC=2∠CAB,∠COB=2∠BAC,
∴∠BAD=∠BOC,
∵∠DAB=∠OBA+∠EBA,
∴∠BOC=∠OBA+∠EBA,
∴∠EFB=∠EBF,
∴EF=EB.
(3)如图3中,过点O作OH⊥AB,垂足为H,延长BE交HO的延长线于G,作BN⊥CF于N,作CK⊥AD于K,连接OA.作CT∠⊥AB于T.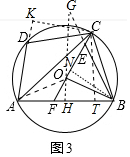
∵∠EBA+∠G=90°,∠CFB+∠HOF=90°,
∵∠EFB=∠EBF,
∴∠G=∠HOF,
∵∠HOF=∠EOG,
∴∠G=∠EOG,
∴EG=EO,
∵OH⊥AB,
∴AB=2HB,
∵OE+EB=AB,
∴GE+EB=2HB,
∴GB=2HB,
∴cos∠GBA=$\frac{HB}{GB}$=$\frac{1}{2}$,
∴∠GBA=60°,
∴△EFB是等边三角形,设HF=a,
∵∠FOH=30°,
∴OF=2FH=2a,
∵AB=13,
∴EF=EB=FB=FH+BH=a+$\frac{13}{2}$,
∴OE=EF-OF=FB-OF=$\frac{13}{2}$-a,OB=OC=OE+EC=$\frac{13}{2}$-a+2=$\frac{17}{2}$-a,
∵NE=$\frac{1}{2}$EF=$\frac{1}{2}$a+$\frac{13}{4}$,
∴ON=OE=EN=($\frac{13}{2}$-a)-($\frac{1}{2}$a+$\frac{13}{4}$)=$\frac{13}{4}$-$\frac{3}{2}$a,
∵BO2-ON2=EB2-EN2,
∴($\frac{17}{2}$-a)2-($\frac{13}{4}$-$\frac{3}{2}$a)2=(a+$\frac{13}{2}$)2-($\frac{1}{2}$a+$\frac{13}{4}$)2,
解得a=$\frac{3}{2}$或-10(舍弃),
∴OE=5,EB=8,OB=7,
∵∠K=∠ATC=90°,∠KAC=∠TAC,AC=AC,
∴△ACK≌△ACT,
∴CK=CT,AK=AT,
∵$\widehat{DC}$=$\widehat{BC}$,
∴DC=BC,
∴Rt△DKC≌Rt△BTC,
∴DK=BT,
∵FT=$\frac{1}{2}$FC=5,
∴DK=TB=FB-FT=3,
∴AK=AT=AB-TB=10,
∴AD=AK-DK=10-3=7.
点评 本题考查圆综合题、圆周角定理、等边三角形的判定和性质、全等三角形的判定和性质、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
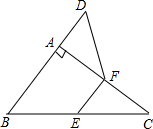 如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=$\frac{1}{2}$AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=$\frac{1}{2}$AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
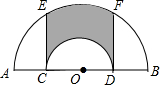 如图,在半圆AOB中,点C为半径OA的中点,以O为圆心,OC为半径画半圆交OB于点D,分别过点C、D作CE、DF垂直AB,交圆O于点E、F,若OA=2,则阴影部分的面积为$\frac{3π}{2}$.
如图,在半圆AOB中,点C为半径OA的中点,以O为圆心,OC为半径画半圆交OB于点D,分别过点C、D作CE、DF垂直AB,交圆O于点E、F,若OA=2,则阴影部分的面积为$\frac{3π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,AB=6,分别以A、B、C、D为圆心,以正方形的边长为半径画弧,弧的交点设为E,F,G,H,则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2.
如图,在正方形ABCD中,AB=6,分别以A、B、C、D为圆心,以正方形的边长为半径画弧,弧的交点设为E,F,G,H,则图中阴影部分的面积是$\frac{3+π-3\sqrt{3}}{3}$a2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
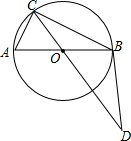 如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2$\sqrt{3}$.
如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com