
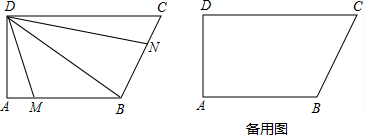
分析 (1)由tan∠ABD=$\frac{AD}{AB}$=$\frac{\sqrt{3}}{3}$,推出∠ABD=30°,由AB∥CD,推出∠CDB=∠ABD=30°,由∠C=90°,推出∠DBC=90°即可.
(2)于△DAM∽△DBN,推出$\frac{DA}{DB}$=$\frac{AM}{BN}$=$\frac{DM}{DN}$,可以推出$\frac{AM}{BN}$=$\frac{DM}{DN}$=$\frac{1}{2}$,由此即可解决问题.
(3)由(2)可知DN=2DM,取DN的中点K,连接MK,首先证明△DMK是等边三角形,推出△DMN是直角三角形,于DM=MN•tan30°=$\frac{\sqrt{39}}{2}$×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{13}}{2}$,
再根据勾股定理求出AM即可解决问题.
解答 解:(1)∵AB∥DC,∠A=90°,
∴∠ADC=180°-∠A=90°,
∵AB=3,AD=$\sqrt{3}$,
∴tan∠ABD=$\frac{AD}{AB}$=$\frac{\sqrt{3}}{3}$,
∴∠ABD=30°,
∴∠CDB=∠ABD=30°,
∵∠C=60°,
∴∠DBC=180°-∠C-∠BDC=90°,
∴BD⊥CB.
(2)∵∠ADB=∠MDN=60°,
∴∠ADM=∠BDN,
∵∠A=∠DBN=90°,
∴△DAM∽△DBN,
∴$\frac{DA}{DB}$=$\frac{AM}{BN}$=$\frac{DM}{DN}$
∵BD=2AD=2$\sqrt{3}$,
∴BC=2,
∴$\frac{AM}{BN}$=$\frac{DM}{DN}$=$\frac{1}{2}$,
∴BN=2AM,
∴2-y=2(3-x),
∴y=2x-4,(2≤x≤3).
(3)由(2)可知DN=2DM,取DN的中点K,连接MK.
∵DM=DK,∠MDK=60°,
∴△DMK是等边三角形,
∴KM=DK=KN,
∴△DMN是直角三角形,
∴∠DNM=30°,
∵MN=$\frac{\sqrt{39}}{2}$,
∴DM=MN•tan30°=$\frac{\sqrt{39}}{2}$×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{13}}{2}$,
∴AM=$\sqrt{D{M}^{2}-A{D}^{2}}$=$\sqrt{(\frac{\sqrt{13}}{2})^{2}-(\sqrt{3})^{2}}$=$\frac{1}{2}$,
∴BN=2AM=1,
∴CN=BC-BN=2-1=1.
点评 本题考查四边形综合题、直角梯形的性质、相似三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活应用所学知识解决问题,正确寻找相似三角形是突破口,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 如图,以△ABC的一边BC为直径的⊙O,交AB于点D,连接CD,OD,已知∠A+$\frac{1}{2}$∠1=90°.
如图,以△ABC的一边BC为直径的⊙O,交AB于点D,连接CD,OD,已知∠A+$\frac{1}{2}$∠1=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 矩形一边长/米 | 5 | 10 | 15 | 20 |
| 矩形面积/m2 | 125 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
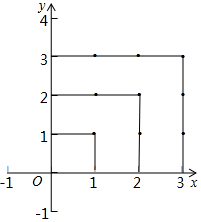 一个粒子在第一象限运动,在第一秒钟内它从原点运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向或在x轴、y轴上来回运动,且每秒移动1个单位长度.
一个粒子在第一象限运动,在第一秒钟内它从原点运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向或在x轴、y轴上来回运动,且每秒移动1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如表:
寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如表:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com