
如图,直线![]() 与x轴交于点A,与y轴交于点B,以线段AB为直径作⊙C,抛物线
与x轴交于点A,与y轴交于点B,以线段AB为直径作⊙C,抛物线![]() 过A、C、O三点.
过A、C、O三点.
(1) 求点C的坐标和抛物线的解析式;
(2) 过点B作直线与x轴交于点D,且OB2=OA·OD,求证:DB是⊙C的切线;
(3) 抛物线上是否存在一点P, 使以P、O、C、A为顶点的四边形为直角梯形,如果存在,求出点P的坐标;如果不存在,请说明理由.
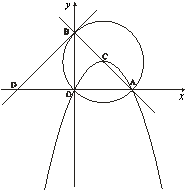
解:(1)A(6,0),B(0,6) ……………………1分
连结OC,由于∠AOB=90o,C为AB的中点,则![]() ,
,
所以点O在⊙C上(没有说明不扣分).
过C点作CE⊥OA,垂足为E,则E为OA中点,故点C的横坐标为3.
又点C在直线y=-x+6上,故C(3,3) ……………………2分
抛物线过点O,所以c=0,
又抛物线过点A、C,所以![]() ,解得:
,解得:![]()
所以抛物线解析式为![]() …………………3分
…………………3分
(2)OA=OB=6代入OB2=OA·OD,得OD=6 ……………………4分
所以OD=OB=OA,∠DBA=90o. ……………………5分
又点B在圆上,故DB为⊙C的切线 ……………………6分
(通过证相似三角形得出亦可)
(3)假设存在点P满足题意.因C为AB中点,O在圆上,故∠OCA=90o,
要使以P、O、C、A为顶点的四边形为直角梯形,
则 ∠CAP=90o或 ∠COP=90o, ……………………7分
若∠CAP=90o,则OC∥AP,因OC的方程为y=x,设AP方程为y=x+b.
又AP过点A(6,0),则b=-6, ……………………8分
方程y=x-6与![]()
![]() 联立解得:
联立解得:![]() ,
,![]() ,
,
故点P1坐标为(-3,-9) ……………………9分
若∠COP=90o,则OP∥AC,同理可求得点P2(9,-9)
(用抛物线的对称性求出亦可)
故存在点P1坐标为(-3,-9)和P2(9,-9)满足题意.…………10分


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
 (2013•南宁)如图,直线y=
(2013•南宁)如图,直线y=| 1 |
| 2 |
| k |
| x |
| 1 |
| 2 |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源:2012届九年级上学期期末数学试卷 题型:选择题
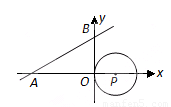
如图,直线 与
与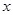 轴、
轴、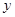 轴分别相交于
轴分别相交于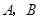 两点,圆心
两点,圆心 的坐标为
的坐标为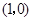 ,圆
,圆 与
与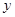 轴相切于点
轴相切于点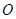 .若将圆
.若将圆 沿
沿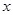 轴向左移动,当圆
轴向左移动,当圆 与该直线相交时,横坐标为整数的点
与该直线相交时,横坐标为整数的点 的个数是( )
的个数是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于
轴分别相交于![]() 两点,圆心
两点,圆心![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() .若将圆
.若将圆![]() 沿
沿![]() 轴向左移动,当圆
轴向左移动,当圆![]() 与该直线相交时,横坐标为整数的点
与该直线相交时,横坐标为整数的点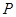 的个数是( )
的个数是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com