
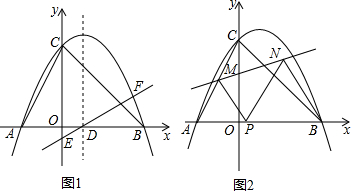
ЗжЮі ЃЈ1ЃЉСюx=0ЕУЃЌy=4ЃЌЧѓГіЕуCЃЈ0ЃЌ4ЃЉЃЌИљОнOB=OC=4ЃЌЕУЕНЕуBЃЈ4ЃЌ0ЃЉДњШыХзЮяЯпБэДяЪНЧѓГіaЕФжЕЃЌМДПЩНтД№ЃЛ
ЃЈ2ЃЉЙ§ЕуMзїMGЁЭxжсгкGЃЌЙ§ЕуNзїNHЁЭxжсгкHЃЌЩшPЃЈxЃЌ0ЃЉЃЌЁїPMNЕФУцЛ§ЮЊSЃЌЗжБ№БэЪОГіPG=$\frac{2+x}{2}$ЃЌMG=$\frac{{\sqrt{3}}}{2}ЃЈ{2+x}ЃЉ$ЃЌPH=$\frac{4-x}{2}$ЃЌNH=$\frac{{\sqrt{3}}}{2}ЃЈ{4-x}ЃЉ$ЃЌИљОнS=SЬнаЮMGHN-SЁїPMG-SЁїPNH=$-\frac{{\sqrt{3}}}{4}{ЃЈ{x-1}ЃЉ^2}+\frac{{9\sqrt{3}}}{2}$ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЕБx=1ЪБЃЌSгазюДѓжЕЪЧ$\frac{{9\sqrt{3}}}{2}$ЃЌМДПЩНтД№ЃЛ
ЃЈ3ЃЉДцдкЕуFЃЌЪЙЕУЁїDOEгыЁїAOCЯрЫЦЃЎгаСНжжПЩФмЧщПіЃКЂйЁїDOEЁзЁїAOCЃЛЂкЁїDOEЁзЁїCOAЃЌЯШЧѓГіЕуEЕФзјБъЃЌдйЧѓГіжБЯпDEЕФНтЮіЪНЃЌРћгУЗНГЬзщЧѓГіЕуFЕФзјБъЃЌМДПЩНтД№ЃЎ
НтД№ НтЃКЃЈ1ЃЉСюx=0ЕУЃЌy=4ЃЌЁрCЃЈ0ЃЌ4ЃЉ
ЁрOB=OC=4ЃЌЁрBЃЈ4ЃЌ0ЃЉ
ДњШыХзЮяЯпБэДяЪНЕУЃК
16a-8a+4=0ЃЌНтЕУa=$-\frac{1}{2}$
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊ$y=-\frac{1}{2}{x^2}+x+4$
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуMзїMGЁЭxжсгкGЃЌЙ§ЕуNзїNHЁЭxжсгкHЃЌ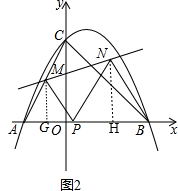
гЩХзЮяЯп$y=-\frac{1}{2}{x^2}+x+4$ЕУЃКAЃЈ-2ЃЌ0ЃЉЃЌ
ЩшPЃЈxЃЌ0ЃЉЃЌЁїPMNЕФУцЛ§ЮЊSЃЌ
дђPG=$\frac{2+x}{2}$ЃЌMG=$\frac{{\sqrt{3}}}{2}ЃЈ{2+x}ЃЉ$ЃЌPH=$\frac{4-x}{2}$ЃЌNH=$\frac{{\sqrt{3}}}{2}ЃЈ{4-x}ЃЉ$
ЁрS=SЬнаЮMGHN-SЁїPMG-SЁїPNH
=$\frac{1}{2}ЃЈ{MG+NH}ЃЉЁСGH-\frac{1}{2}PGЁСMG-\frac{1}{2}PHЁСNH$
=$-\frac{{\sqrt{3}}}{4}{x^2}+\frac{{\sqrt{3}}}{2}x+2\sqrt{3}$
=$-\frac{{\sqrt{3}}}{4}{ЃЈ{x-1}ЃЉ^2}+\frac{{9\sqrt{3}}}{2}$
Ёп$-\frac{{\sqrt{3}}}{4}ЃМ0$ЃЌ
ЁрЕБx=1ЪБЃЌSгазюДѓжЕЪЧ$\frac{{9\sqrt{3}}}{2}$
ЁрЁїPMNЕФзюДѓУцЛ§ЪЧ$\frac{{9\sqrt{3}}}{2}$ЃЌДЫЪБЕуPЕФзјБъЪЧЃЈ1ЃЌ0ЃЉ
ЃЈ3ЃЉДцдкЕуFЃЌЪЙЕУЁїDOEгыЁїAOCЯрЫЦЃЎгаСНжжПЩФмЧщПіЃК
ЂйЁїDOEЁзЁїAOCЃЛЂкЁїDOEЁзЁїCOA
гЩХзЮяЯп$y=-\frac{1}{2}{x^2}+x+4$ЕУЃКAЃЈ-2ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпx=1ЃЌ
ЁрOA=2ЃЌOC=4ЃЌOD=1
ЂйШєЁїDOEЁзЁїAOCЃЌдђ$\frac{OD}{OA}=\frac{OE}{OC}$
Ёр$\frac{1}{2}=\frac{OE}{4}$ЃЌ
НтЕУOE=2
ЁрЕуEЕФзјБъЪЧЃЈ0ЃЌ2ЃЉЛђЃЈ0ЃЌ-2ЃЉ
ШєЕуEЕФзјБъЪЧЃЈ0ЃЌ2ЃЉЃЌ
дђжБЯпDEЮЊЃКy=-2x+2
НтЗНГЬзщ$\left\{\begin{array}{l}y=-2x+2\\ y=-\frac{1}{2}{x^2}+x+4\end{array}\right.$
ЕУЃК$\left\{\begin{array}{l}{x_1}=3+\sqrt{13}\\{y_1}=-4-2\sqrt{13}\end{array}\right.$ЃЌ$\left\{\begin{array}{l}{x_2}=3-\sqrt{13}\\{y_2}=-4+2\sqrt{13}\end{array}\right.$ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
ДЫЪБТњзуЬѕМўЕФЕуF1ЕФзјБъЮЊЃЈ$3+\sqrt{13}$ЃЌ$-4-2\sqrt{13}$ЃЉ
ШєЕуEЕФзјБъЪЧЃЈ0ЃЌ-2ЃЉЃЌ
ЭЌРэПЩЧѓЕУТњзуЬѕМўЕФЕуF2ЕФзјБъЮЊЃЈ$-1+\sqrt{13}$ЃЌ$-3+2\sqrt{13}$ЃЉ
ЂкШєЁїDOEЁзЁїCOAЃЌ
ЭЌРэвВПЩЧѓЕУТњзуЬѕМўЕФЕуF3ЕФзјБъЮЊЃЈ$\frac{{\sqrt{37}+3}}{2}$ЃЌ$-\frac{{\sqrt{37}+1}}{4}$ЃЉ
ТњзуЬѕМўЕФЕуF4ЕФзјБъЮЊЃЈ$\frac{{\sqrt{37}+1}}{2}$ЃЌ$\frac{{\sqrt{37}-1}}{4}$ЃЉ
злЩЯЫљЪіЃЌДцдкТњзуЬѕМўЕФЕуFЃЌЕуFЕФзјБъЮЊЃК
F1ЃЈ$3+\sqrt{13}$ЃЌ$-4-2\sqrt{13}$ЃЉЁЂF2ЃЈ$-1+\sqrt{13}$ЃЌ$-3+2\sqrt{13}$ЃЉЁЂF3ЃЈ$\frac{{\sqrt{37}+3}}{2}$ЃЌ$-\frac{{\sqrt{37}+1}}{4}$ЃЉЛђF4ЃЈ$\frac{{\sqrt{37}+1}}{2}$ЃЌ$\frac{{\sqrt{37}-1}}{4}$ЃЉЃЎ
ЕуЦР БОЬтПМВщСЫЖўДЮКЏЪ§ЕФаджЪЁЂЯрЫЦШ§НЧаЮЕФаджЪгыХаЖЈЃЌдкЃЈ2ЃЉжаРћгУЖўДЮКЏЪ§ЕФаджЪНтОізюжЕЮЪЬтЪЧЙиМќЃЌдкЃЈ3ЃЉжаЗжРрЬжТлЫМЯыЕФгІгУЪЧНтОіБОЬтЕФЙиМќЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
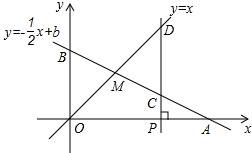 ШчЭМЫљЪОЃЌвбжЊКЏЪ§y=-$\frac{1}{2}$x+bЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЌгыКЏЪ§y=xЕФЭМЯѓНЛгкЕуMЃЌЕуMЕФКсзјБъЮЊ2ЃЌдкxжсЩЯгавЛЕуPЃЈaЃЌ0ЃЉЃЈЦфжаaЃО2ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌЗжБ№НЛКЏЪ§y=-$\frac{1}{2}$x+bКЭy=xЕФЭМЯѓгкЕуCЃЌDЃЎ
ШчЭМЫљЪОЃЌвбжЊКЏЪ§y=-$\frac{1}{2}$x+bЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЌгыКЏЪ§y=xЕФЭМЯѓНЛгкЕуMЃЌЕуMЕФКсзјБъЮЊ2ЃЌдкxжсЩЯгавЛЕуPЃЈaЃЌ0ЃЉЃЈЦфжаaЃО2ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌЗжБ№НЛКЏЪ§y=-$\frac{1}{2}$x+bКЭy=xЕФЭМЯѓгкЕуCЃЌDЃЎ ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
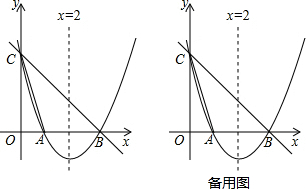
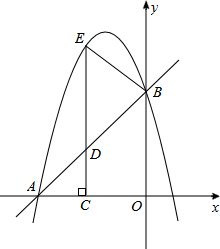 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпy=x+4гыxжсЁЂyжсЗжБ№НЛгкЕуAЃЌBЃЌХзЮяЯпy=-x2+bx+cОЙ§AЁЂBСНЕуЃЌDЃЈmЃЌm+4ЃЉЮЊжБЯпABЩЯвЛЖЏЕуЃЌЙ§ЕуDзїxжсЕФДЙЯпЃЌДЙзуЮЊЕуCЃЌCDЕФбгГЄЯпНЛХзЮяЯпгкЕуEЃЌСЌНгBEЃЎ
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпy=x+4гыxжсЁЂyжсЗжБ№НЛгкЕуAЃЌBЃЌХзЮяЯпy=-x2+bx+cОЙ§AЁЂBСНЕуЃЌDЃЈmЃЌm+4ЃЉЮЊжБЯпABЩЯвЛЖЏЕуЃЌЙ§ЕуDзїxжсЕФДЙЯпЃЌДЙзуЮЊЕуCЃЌCDЕФбгГЄЯпНЛХзЮяЯпгкЕуEЃЌСЌНгBEЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com