
| x2+48 |
| x2+48 |

| a | 2 1 |
| a | 2 2 |
| a | 2 1 |
| a | 2 2 |
| a | 2 1 |
| a | 2 2 |
 解:[定理表述]直角三角形的两条直角边的平方和等于斜边的平方.
解:[定理表述]直角三角形的两条直角边的平方和等于斜边的平方.
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x2-1+49 |
| x2+48 |
| x2+48 |
| a | 2 1 |
| a | 2 2 |
| x2+48 |
| a | 2 1 |
| a | 2 2 |
| a | 2 1 |
| a | 2 2 |
| a | 2 1 |
| a | 2 2 |


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
『问题情境』勾股定理是一条古老的数学定理,它有多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其它星球“人”进行第一次“谈话”的语言.
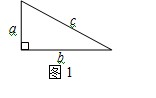
『定理表述』请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述).
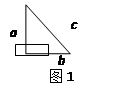
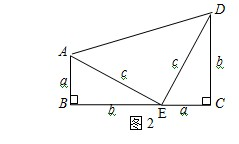
『尝试证明』以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理.
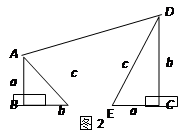
『知识拓展』利用图2中的直角梯形,我们可以证明<.其证明步骤如下:
∵BC=a+b,AD= ,
又在直角梯形ABCD中,BC AD(填大小关系),
即 .
∴<.
查看答案和解析>>
科目:初中数学 来源: 题型:

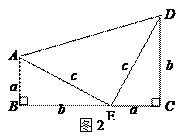
查看答案和解析>>
科目:初中数学 来源:2011年河北省唐山市玉田县八年级第一学期期中考试数学卷 题型:解答题
『问题情境』勾股定理是一条古老的数学定理,它有多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其它星球“人”进行第一次“谈话”的语言.
『定理表述』请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述).
『尝试证明』以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理.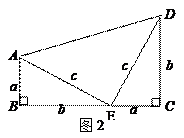
『知识拓展』利用图2中的直角梯形,我们可以证明<.其证明步骤如下:
∵BC=a+b,AD= ,
又在直角梯形ABCD中,BC AD(填大小关系),
即 .
∴<.
查看答案和解析>>
科目:初中数学 来源:2011年河北省唐山市玉田县八年级第一学期期中考试数学卷 题型:解答题
『问题情境』勾股定理是一条古老的数学定理,它有多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其它星球“人”进行第一次“谈话”的语言.
『定理表述』请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述).

『尝试证明』以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理.

『知识拓展』利用图2中的直角梯形,我们可以证明<.其证明步骤如下:
∵BC=a+b,AD= ,
又在直角梯形ABCD中,BC AD(填大小关系),
即 .
∴<.
查看答案和解析>>
科目:初中数学 来源:河北省期中题 题型:解答题
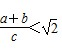 .其证明步骤如下:∵BC=a+b,AD=( ),
.其证明步骤如下:∵BC=a+b,AD=( ),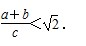 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com