
【题目】已知y1=a1(x﹣m)2+5,点(m,25)在抛物线y2=a2x2+b2x+c2上,其中m>0.
(1)若a1=﹣1,点(1,4)在抛物线y1=a1(x﹣m)2+5上,求m的值;
(2)记O为坐标原点,抛物线y2=a2x2+b2x+c2的顶点为M,若c2=0,点A(2,0)在此抛物线上,∠OMA=90°,求点M的坐标;
(3)若y1+y2=x2+16x+13,且4a2c2﹣b22=﹣8a2,求抛物线y2=a2x2+b2x+c2的解析式.
【答案】(1)m=2;(2)M(1,﹣1);(3)y2=3x2+12x+10.
【解析】试题分析:(1)把点代入求值.(2)把已知点代入可求得抛物线对称轴,由对称性可知△OAM是等腰三角形,所以可以得到M点坐标.
(3)利用待定系数法,结合已知联立方程组求解,利用代入消元技巧,可求得抛物线解析式.
试题解析:
(1)∵a1=﹣1,∴y1=﹣(x﹣m)2+5.
将(1,4)代入y1=﹣(x﹣m)2+5,得
4=﹣(1﹣m)2+5.
m=0或m=2.∵m>0,∴m=2.
(2)∵c2=0,∴抛物线y2=a2 x2+b2 x,
将(2,0)代入y2=a2 x2+b2 x,得4a2+2b2=0.即b2=﹣2a2,
∴抛物线的对称轴是x=1,
设对称轴与x轴交于点N,根据抛物线的对称性得,△OAM是等腰三角形,
∴NA=NO=1,
∵∠OMA=90°,
∴MN=OA=1,∴当a2>0时,M(1,﹣1),
当a2<0时,M(1,1),
∵25>1,∴M(1,﹣1).
(3)方法一:∵点(m,25)在抛物线y2=a2 x2+b2x+c2上,
∴a2 m 2+b2 m+c2=25①,
∵y1+y2=(a1+a2)x2+(b2﹣2a1m)x+5+a1m2+c2=x2+16x+13,
∴a1+a2=1②,b2﹣2a1m=16③,a1m2+c2=8④,
由③得,b2m=16m+2a1m2⑤,由④得,c2=8a1m2⑥,
将⑤⑥代入方程①得,a2 m 2+16m+2 m 2 a1+8﹣m 2 a1=25,
整理得,m 2+16m﹣17=0,
解得m1=1,m2=﹣17,
∵m>0,∴m=1,
将m=1代入③得,b2=16+2a1=12+2(1﹣a2)=18﹣2a2,将m=1代入④得,c2=8﹣a1=8﹣(1﹣a2)=7+a2.
∵4a2 c2﹣b22=﹣8a2,∴4a2(7+a2)﹣(18﹣2a2)2=﹣8a2,
∴a2=3,∴b2=18﹣2×3=12,c2=7+3=10,
∴抛物线y2=a2x2+b2x+c2的解析式为y=3x2+12x+10.
方法二,由题意知,当x=m时,y1=5;当x=m时,y2=25,
∴当x=m时,y1+y2=5+25=30,
∵y1+y2=x2+16 x+13,∴30=m2+16m+13.
解得m1=1,m2=﹣17.
∵m>0,∴m=1,
∵4a2 c2﹣b22=﹣8a2,∴ ![]() =
=![]() =﹣2,
=﹣2,
∴y2 顶点的纵坐标为﹣2,
设抛物线y2的解析式为y2=a2 (x﹣h)2﹣2,∴y1+y2=a1 (x﹣1)2+5+a2 (x﹣h)2﹣2.
∵y1+y2=(a1+a2)x2﹣2(a1+a2h)x+a1+a2h2+3=x2+16 x+13,∴a1+a2=1①,﹣2(a1+a2h)=16②,a1+a2h2+3=13③,将①代入②③化简得,a2h﹣a2=﹣9④,a2h2﹣a2=9⑤,联立④⑤,解得h=﹣2,a2=3,
∴抛物线的解析式为y2=3(x+2)2﹣2=3x2+12x+10.
方法三、由题意知,当x=m时,y1=5;当x=m时,y2=25,
∴当x=m时,y1+y2=5+25=30,
∵y1+y2=x2+16x+13,∴30=m2+16m+13,
∴m=1或m=﹣17,∵m>0,∴m=1,∴y1=a1 (x﹣1)+5,
∵y1+y2=x2+16x+13,∴y2=x2+16 x+13﹣y1
=x2+16x+13﹣a1 (x﹣1)2﹣5,
即y2=(1﹣a1)x2+(16+2a1)x+8﹣a1,
∵4a2c2﹣b22=﹣8a2,∴ ![]() =
=![]() =﹣2,
=﹣2,
∴y2 顶点的纵坐标为﹣2,∴ 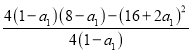 =-2,
=-2,
∴a1=﹣2,∴y2=3x2+12x+10.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】(本题满分10分)沿海开发公司准备投资开发A、B两种新产品,通过市场调研发现:
(1)若单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;
(2)若单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
(3)根据公司信息部的报告,yA,yB(万元)与投资金额x(万元)的部分对应值如下表所示:

(1)填空:yA= ;yB= ;
(2)若公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),试写出W与某种产品的投资金额x(万元)之间的函数关系式;
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润 = 销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;

(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月1日,某园林公司派出一批工人去完成种植2200棵景观树木的任务,这批工人3月1日到5日种植的数量(单位:棵)如图所示.

(1)这批工人前两天平均每天种植多少棵景观树木?
(2)因业务需要,到3月10日必须完成种植任务,你认为该园林公司是否需要增派工人?请运用统计知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l,2表示两人离A地的距离s(m)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示甲离A地的距离与时间关系的图象是 (填l1或l2);甲的速度是 (km/h);乙的速度是 (km/h);
(2)甲出发多长时间后两人相遇?(利用方程解决)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系:

解:CD⊥AB
∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠_____=90°(垂直定义)
∴DG∥AC,(____________________)
∴∠2=∠_________.(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠________(等量代换)
∴EF∥______(同位角相等,两直线平行)
∴∠AEF=∠ADC,(________________)
∵EF⊥AB,
∴∠AEF=90°
∴∠ADC=90°
即:CD⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,得到Cn,若点P(2017,m)在抛物线Cn上,则m为( )
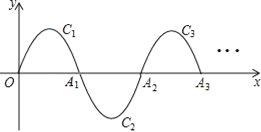
A. 1 B. ﹣1 C. 2 D. ﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC和△DCE中,∠ACB=∠DCE=90°,AC=DC,BC=EC,AB与DE相交于点F.
(1)如图1,求证AB=DE;
(2)如图2,连接CF,求证∠AFC=∠EFC;
(3)如图3,在(2)的条件下,当AF=EF时,连接BD,AE,延长CF交BD于点G,AE交CF于点H,若AE=8,BG=2,求线段GH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com