
【题目】定义:有一组对角互补的四边形叫做互补四边形.
![]() 概念理解:
概念理解:
①在互补四边形![]() 中,
中,![]() 与
与![]() 是一组对角,若
是一组对角,若![]() 则
则![]() _
_ ![]()
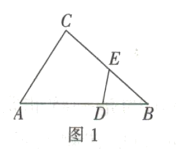
②如图1,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() 求证:四边形
求证:四边形![]() 是互补四边形.
是互补四边形.
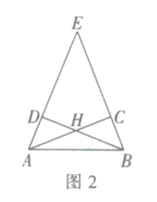
![]() 探究发现:如图2,在等腰
探究发现:如图2,在等腰![]() 中,
中,![]() 点
点![]() 分别在边
分别在边![]() 上,
上, ![]() 四边形
四边形![]() 是互补四边形,求证:
是互补四边形,求证:![]() .
.
![]() 推广运用:如图3,在
推广运用:如图3,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,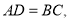 四边形
四边形![]() 是互补四边形,若
是互补四边形,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)①90;②见解析;(2)见解析;(3)![]() .
.
【解析】
(1)①由互补四边形和四边形内角和定理即可求出∠A的度数;
②证明![]() 得
得![]() ,进而可得
,进而可得![]() ,从而可证明四边形
,从而可证明四边形![]() 是互补四边形;
是互补四边形;
(2)先证明![]() 得
得![]() ,根据EA=EB可得
,根据EA=EB可得![]() ,根据三角形内角和定理得∠AHB=180°-(
,根据三角形内角和定理得∠AHB=180°-(![]() ),再根据互补四边形的定义可得结论;
),再根据互补四边形的定义可得结论;
(3)如图,作![]() 于点
于点![]() 交
交![]() 的延长线于点
的延长线于点![]() 则
则![]() ,由四边形CEDH是互补四边形可得
,由四边形CEDH是互补四边形可得![]() ,进而证明
,进而证明![]() ,
,![]() ,求得
,求得![]() ,再证明
,再证明![]() 即可得到结论.
即可得到结论.
(1)①解:∵四边形ABCD是互补四边形,
∴∠B+∠D=180°,
∵∠B:∠C:∠D=2:3:4,
∴∠B=60°,∠C=90°,
又∵∠A+∠B+∠C+∠D=360°,
∴∠A=180°-∠C=90°;
故答案为:90;
②证明:![]()
![]()
又![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是互补四边形.
是互补四边形.
![]() 证明:
证明:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是互补四边形,
是互补四边形,![]()
![]()
![]()
![]() 如图,作
如图,作![]() 于点
于点![]() 交
交![]() 的延长线于点
的延长线于点![]()
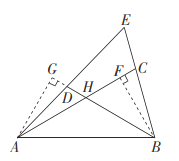
则![]()
![]() 四边形
四边形![]() 是互补四边形,
是互补四边形,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
在![]() 中,
中,![]()
![]() 设
设![]() 则
则![]()
![]()
![]()
![]()
![]() .
.
![]() ,
,
![]()
![]()


科目:初中数学 来源: 题型:
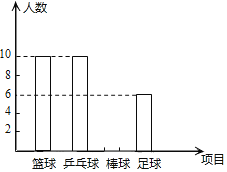
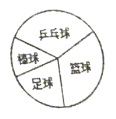
【题目】为丰富同学们的校园生活,某校积极开展了体育类、文艺类、文化类等形式多样的社团活动(每人仅限参加一项).李老师在九年级随机抽取了2个班级,对这2个班级参加体育类社团活动的人数情况进行了统计,并绘制了下面的统计图.已知这2个班级共有![]() 的学生参加“足球”项目,且扇形统计图中“足球”项目扇形圆心角为
的学生参加“足球”项目,且扇形统计图中“足球”项目扇形圆心角为![]() .
.
(1)这2个班参加体育类社团活动人数为______;
(2)请在图中将表示“棒球”项目的图形补充完整;
(3)若该校九年级共有600名学生,请你根据上述信息估计该校九年级共有多少名学生参加“棒球”项目?
(4)小明和小刚都是这2个班的学生,且都参加了体育类社团活动,请用列表或树状图法求小明和小刚都参加足球社团的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列8×8的网格中,横、纵坐标均为整点的数叫做格点,△ABC的顶点的坐标分别为A(3,0)、B(0,4)、C(4,2).
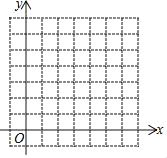
(1)直接写出△ABC的形状;
(2)要求在下图中仅用无刻度的直尺作图:将△ABC绕点B逆时针旋转角度2α得到△A1BC1,其中α=∠ABC,A、C的对应点分别为A1、C1,请你完成作图;
(3)在网格中找一个格点G,使得C1G⊥AB,并直接写出G点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组学过锐角三角函数后,到市龙源湖公园测量塑像“夸父追日”的高度,如图所示,在A处测得塑像顶部D的仰角为45°,塑像底部E的仰角为30.1°,再沿AC方向前进10m到达B处,测得塑像顶部D的仰角为59.1°.求塑像“夸父追日”DE高度.(结果精确到0.1m.参考数据:sin30.1°≈0.50,cos30.1°≈0.87,tan30.1°≈0.58,sin59.1°≈0.86,cos59.1°≈0.51,tan59.1°≈1.67)

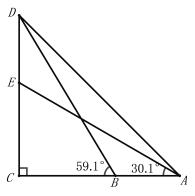
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格纸中,![]() 、
、![]() 都是格点,以
都是格点,以![]() 为圆心,
为圆心,![]() 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
(1)在圆①中画圆![]() 的一个内接正六边形
的一个内接正六边形![]() ;
;
(2)在图②中画圆![]() 的一个内接正八边形
的一个内接正八边形![]() .
.
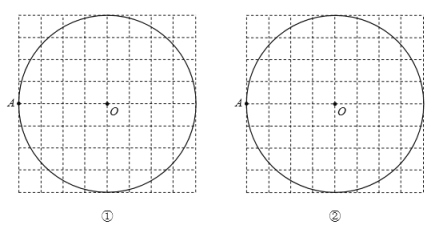
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为半圆O的直径,过点B作PB⊥OB,连接AP交半圆O于点C,D为BP上一点,CD是半圆O的切线.
(1)求证:CD=DP.
(2)已知半圆O的直径为![]() ,PC=1,求CD的长.
,PC=1,求CD的长.
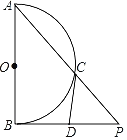
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O.若BO=6,PO=2,则AP的长,AO的长分别为__________.
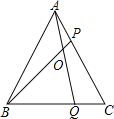
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情.疫情期间,某企业员工积极参加献爱心活动,该企业率先捐款的50名员工的捐款情况统计如下表:
金额/元 | 50 | 100 | 200 | 500 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的平均数、中位数、众数分别是( )
A.276,100,200B.276,200,100C.370,100,100D.370,200,100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过点A(2,﹣3).
(1)如图,过点A分别向x轴,y轴作垂线,垂足分别为B,C,得到矩形ABOC,且抛物线经过点C.
①求抛物线的解析式.
②将抛物线向左平移m(m>0)个单位,分别交线段OB,AC于D,E两点.若直线DE刚好平分矩形ABOC的面积,求m的值.
(2)将抛物线平移,使点A的对应点为A1(2﹣n,3b),其中n≥1.若平移后的抛物线仍然经过点A,求平移后的抛物线顶点所能达到最高点时的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com