

分析 (1)根据条形统计图中的数据求出调查的居民人数即可;
(2)根据总人数减去爱吃A、B、D三种粽子的人数可得爱吃C的人数,然后再根据人数计算出百分比即可;
(3)求出D占的百分比,乘以8000即可得到结果;
(4)画树状图得出所有等可能的情况数,找出他第二个吃到的恰好是C粽的情况数,即可求出所求的概率.
解答 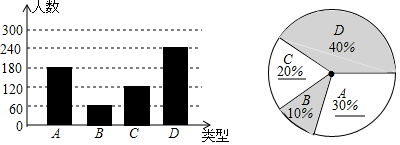 解:(1)根据题意得:180+60+120+240=600(人);
解:(1)根据题意得:180+60+120+240=600(人);
(2)如图所示;
(3)根据题意得:40%×8000=3200(人);
(4)如图,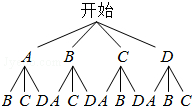
得到所有等可能的情况有12种,其中第二个吃到的恰好是C粽的情况有3种,
则P(C粽)=$\frac{3}{12}$=$\frac{1}{4}$,
答:他第二个吃到的恰好是C粽的概率是$\frac{1}{4}$.
点评 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
| A. | 40×10-9米 | B. | 4×10-8米 | C. | 4×10-10米 | D. | 0.4×10-9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.8592×109 | B. | 2.8592×1010 | C. | 2.8592×1011 | D. | 2.8592×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 4 | 12 | 16 | 17 | 1 |
| A. | 17,16 | B. | 3,2.5 | C. | 2,3 | D. | 3,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 时间段 | 7~8 | 8~9 | 9~10 | 10~11 | 11~12 |
| 人数 | 20 | 15 | 10 | 15 | 40 |
| A. | 10人,15人 | B. | 15人,15人 | C. | 15人,20人 | D. | 10人,20人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
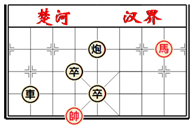 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )| A. | (-3,3) | B. | (0,3) | C. | (3,2) | D. | (1,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com