
 解:(1)容易把一个正方形分成42=16个正方形,再把其中位于一角的9个拼成一个正方形,
解:(1)容易把一个正方形分成42=16个正方形,再把其中位于一角的9个拼成一个正方形,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
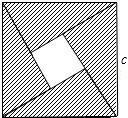
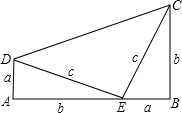
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
(2)试设计一种方法,把一个大立方体分割成55个小立方体.
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学九年级上6.3池塘里有多少条鱼练习卷(解析版) 题型:解答题
一盘残棋,小明通过数右上角一部分白棋子占60%,他又数了白棋子一共是87个,从而算出黑棋子大约有58个.
(1)你同意这种估算方法吗?说明理由.
(2)你有更合理的估算方法吗?试设计一种方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com