
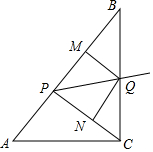
 如图,已知在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,ON⊥CP于N.
如图,已知在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,ON⊥CP于N.分析 (1)根据AP=CP,∠ACB=90°,可得BP=CP,再根据PQ平分∠BPC,可得Q是BC的中点,而P是AB的中点,即可得出PQ=$\frac{1}{2}$AC=3;
(2)先根据面积法求得PC=$\frac{24}{5}$,再设AP=x,根据勾股定理可得方程62-x2=82-(10-x)2,解得x=$\frac{18}{5}$,求得BP=$\frac{32}{5}$,再根据△BMQ∽△BPC,得出$\frac{PB}{PC}$=$\frac{BM}{MQ}$=$\frac{BM}{MP}$=$\frac{BQ}{QC}$,即CQ=$\frac{PC×BQ}{BP}$,进而得出CQ=$\frac{3}{4}$(8-CQ),解得CQ=$\frac{24}{7}$;
(3)根据∠B=∠QPC,∠PCQ=∠BCP,即可判定△CPQ∽△CBP,进而得到$\frac{CP}{BC}$=$\frac{CQ}{CP}$=$\frac{PQ}{BP}$①,可得CP=5,由①可得,CQ=$\frac{25}{8}$,即可得到BQ=$\frac{39}{8}$,再求得Rt△BMQ中,BM=BQ×cosB=$\frac{39}{10}$,即可得到AP=AB-2BM=$\frac{11}{5}$.
解答  解:(1)在Rt△ABC中,AB=10,sinA=$\frac{4}{5}$,
解:(1)在Rt△ABC中,AB=10,sinA=$\frac{4}{5}$,
∴BC=AB×sinA=8,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6,
∵AP=CP,
∴∠A=∠PCA,
∵∠ACB=90°,
∴∠A+∠B=90°,∠ACP+∠BCP=90°,
∴∠B=∠BCP,
∴BP=CP,
又∵PQ平分∠BPC,
∴Q是BC的中点,
又∵BP=CP=AP,
∴P是AB的中点,
∴PQ=$\frac{1}{2}$AC=3;
(2)∵CP⊥AB,∠ACB=90°,
∴$\frac{1}{2}$×AB×CP=$\frac{1}{2}$×AC×BC,
∴PC=$\frac{AC×BC}{AB}$=$\frac{24}{5}$,
设AP=x,则
Rt△ACP中,PC2=62-x2,
Rt△BCP中,PC2=82-(10-x)2,
∴62-x2=82-(10-x)2,
解得x=$\frac{18}{5}$,
∴BP=10-$\frac{18}{5}$=$\frac{32}{5}$,
又∵CP⊥AB,QM⊥AB,
∴QM∥CP,
∴△BMQ∽△BPC,
∴$\frac{PB}{PC}$=$\frac{BM}{MQ}$=$\frac{BM}{MP}$=$\frac{BQ}{QC}$,
∴CQ=$\frac{PC×BQ}{BP}$,即CQ=$\frac{3}{4}$(8-CQ),
解得CQ=$\frac{24}{7}$;
(3)由角平分线的性质易得S△PMQ=S△PNQ=$\frac{1}{2}$×PM×QM,
∵四边形PMQN与△BPQ的面积相等,
∴PM×QM=$\frac{1}{2}$BP×QM,
∴PM=$\frac{1}{2}$BP,
∴QM是PB的垂直平分线,
∴∠QPB=∠B,
∵∠QPB=∠QPC,
∴∠B=∠QPC,
又∵∠PCQ=∠BCP,
∴△CPQ∽△CBP,
∴$\frac{CP}{BC}$=$\frac{CQ}{CP}$=$\frac{PQ}{BP}$①,
∴$\frac{CP}{BC}$=$\frac{BQ}{BP}$=$\frac{BQ}{2BM}$,即CP=4×$\frac{BQ}{BM}$=4×$\frac{5}{4}$=5,
由①可得,CQ=$\frac{C{P}^{2}}{BC}$=$\frac{25}{8}$,
∴BQ=8-CQ=$\frac{39}{8}$,
∴Rt△BMQ中,BM=BQ×cosB=$\frac{39}{8}$×$\frac{4}{5}$=$\frac{39}{10}$,
∴AP=AB-2BM=10-2×$\frac{39}{10}$=$\frac{11}{5}$.
点评 本题属于四边形综合题,主要考查了相似三角形的判定与性质,解直角三角形以及勾股定理的综合应用,解题时注意:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
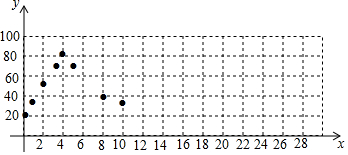
| 接通电源后的时间x (单位:min) | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
| 水箱中水的温度y (单位:℃) | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
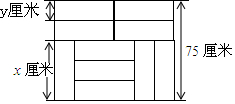 如图,10块相同的长方形墙砖拼成一个矩形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是( )
如图,10块相同的长方形墙砖拼成一个矩形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是( )| A. | $\left\{\begin{array}{l}{x+2y=75}\\{y=3x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=75}\\{x=3y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+y=75}\\{y=3x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+2y=75}\\{x=3y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点确定一条直线 | |
| B. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| C. | 垂线段最短 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
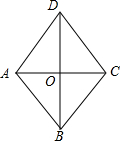 如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=2,若AB=2,则BD的长为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=2,若AB=2,则BD的长为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com