
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(1)求该抛物线的解析式和顶点坐标.
(2)若点![]() 在抛物线上,且点
在抛物线上,且点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
①当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
②当点![]() 落在第二象限内,
落在第二象限内,![]() 取得最小值时,求
取得最小值时,求![]() 的值.
的值.
【答案】(1)![]() ,顶点的坐标为(1,-4);(2)①
,顶点的坐标为(1,-4);(2)①![]() ,
,![]() ;②
;②![]() .
.
【解析】
(1)把坐标代入求出解析式,再化为顶点式即可求解;
(2)①由对称性可表示出P’的坐标,再由P和P’都在抛物线上,可得到m的方程,即可求出m的值;
②由点P’在第二象限,可求出t的取值,利用两点间的距离公式可用t表示![]() ,再由带你P’在抛物线上,可消去m,整理得到关于t的二次函数,利用二次函数的性质即可求出最小值时t的值,则可求出m的值.
,再由带你P’在抛物线上,可消去m,整理得到关于t的二次函数,利用二次函数的性质即可求出最小值时t的值,则可求出m的值.
(1)∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() ,解得
,解得![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
∵![]() ,∴顶点的坐标为
,∴顶点的坐标为![]() .
.
(2)①由点![]() 在抛物线
在抛物线![]() 上,有
上,有![]() .
.
∵![]() 关于原点的对称点为
关于原点的对称点为![]() ,有
,有![]() .
.
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() .
.
②由题意知![]() 在第二象限,∴
在第二象限,∴![]() ,
,![]() ,即
,即![]() ,
,![]() .
.
则![]() 在第四象限.
在第四象限.
∵抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,∴
,∴![]() .
.
过点![]() 作
作![]() 轴,
轴,![]() 为垂足,则
为垂足,则![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
当点![]() 和
和![]() 不重合时,在
不重合时,在![]() 中,
中,![]() .
.
当点![]() 和
和![]() 重合时,
重合时,![]() ,
,![]() ,符合上式.
,符合上式.
∴![]() ,即
,即![]() .
.
记![]() ,则
,则![]() ,
,
∴当![]() 时,
时,![]() 取得最小值.
取得最小值.
把![]() 代入
代入![]() ,得
,得![]() ,
,
解得![]() ,
,![]() ,
,
由![]() ,可知
,可知![]() 不符合题意,∴
不符合题意,∴![]() .
.


科目:初中数学 来源: 题型:
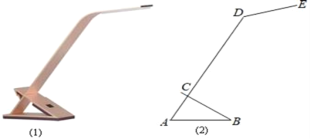
【题目】如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)
(1)求DE与水平桌面(AB所在直线)所成的角;
(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).
查看答案和解析>>
科目:初中数学 来源: 题型:
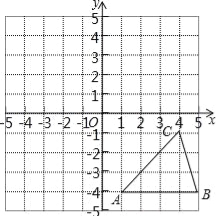
【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
(1)作出△ABC关于y轴对称的![]() ,并写出
,并写出![]() 的坐标;
的坐标;
(2)作出△ABC绕点O逆时针旋转90°后得到的![]() ,并求出
,并求出![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
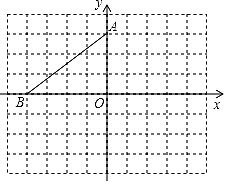
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(0,3)、(-4,0).
(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O、B对应点分别是E、F,请在图中面出△AEF;
(2)以点O为位似中心,将三角形AEF作位似变换且缩小为原来的![]() 在网格内画出一个符合条件的
在网格内画出一个符合条件的![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 的对角线
的对角线![]() 上,
上,![]() 所在的直线交
所在的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() . 下列结论中,正确的有_________ (填序号).
. 下列结论中,正确的有_________ (填序号).
①![]() ;②
;②![]() 是
是![]() 的一个三等分点;③
的一个三等分点;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好全国文明城市的创建工作,我市交警连续![]() 天对某路口
天对某路口![]() 个“
个“![]() 岁以下行人”和
岁以下行人”和![]() 个“
个“![]() 岁及以上行人”中出现交通违章的情况进行了调查统计,将所得数据绘制成如下统计图.请根据所给信息,解答下列问题.
岁及以上行人”中出现交通违章的情况进行了调查统计,将所得数据绘制成如下统计图.请根据所给信息,解答下列问题.
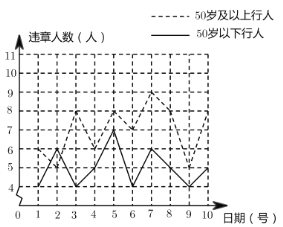
(1)求这![]() 天“
天“![]() 岁及以上行人”中每天违章人数的众数.
岁及以上行人”中每天违章人数的众数.
(2)某天中午下班时段经过这一路口的“![]() 岁以下行人”为
岁以下行人”为![]() 人,请估计大约有多少人会出现交通违章行为.
人,请估计大约有多少人会出现交通违章行为.
(3)请根据以上交通违章行为的调查统计,就文明城市创建减少交通违章提出合理建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+2x+3交x轴于点A、B,其中点A在点B的左边,交y轴于点C,点P为抛物线上位于x轴上方的一点.
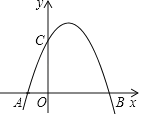
(1)求A、B、C三点的坐标;
(2)若△PAB的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,D是BC的中点,P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则△ABC的面积为( )


A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点,若扇形的半径为![]() ,则图中阴影部分的面积等于_____.
,则图中阴影部分的面积等于_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com