
【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
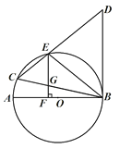
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.
【答案】(1)见解析;(2)BG的长为5.
【解析】
(1)连接AE,根据圆周角定理可得∠BAE=∠BCE,由AB是直径可得∠AEB=90°,进而可得∠BAE+∠ABE=90°,由∠BCD=∠DBE.利用等量代换即可求出∠ABD=90°,可得BD是⊙O的切线;(2)延长EF交⊙O于H,根据垂径定理可得![]() ,进而可得∠ECB=∠BEH,由∠EBC是公共角即可证明△EBC∽△GBE,根据相似三角形的性质可得
,进而可得∠ECB=∠BEH,由∠EBC是公共角即可证明△EBC∽△GBE,根据相似三角形的性质可得![]() ,根据等腰三角形的性质可得∠D=∠BCE,利用等量代换可得∠D=∠DBE,可得BE=DE,由∠AFE=∠ABD=90°可得EF//BD,根据平行线性质可得∠D=∠CEF,即可证明∠BCE=∠CEF,可得CG=GE,即可得出BC=BG+EG,代入
,根据等腰三角形的性质可得∠D=∠BCE,利用等量代换可得∠D=∠DBE,可得BE=DE,由∠AFE=∠ABD=90°可得EF//BD,根据平行线性质可得∠D=∠CEF,即可证明∠BCE=∠CEF,可得CG=GE,即可得出BC=BG+EG,代入![]() 求出BG的长即可.
求出BG的长即可.
(1)如图,连接AE,则∠BAE=∠BCE,
∵AB是直径,
∴∠AEB=90°,
∴∠BAE+∠ABE=90°,
∴∠ABE+∠BCE=90°,
∵∠BCE=∠DBE,
∴∠ABE+∠DBE=90°,即∠ABD=90°,
∴BD是⊙O的切线.
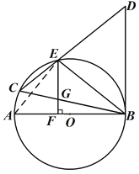
(2)如图,延长EF交⊙O于H,
∵EF⊥AB,AB是直径,
∴![]() ,
,
∴∠ECB=∠BEH,
∵∠EBC=∠GBE,
∴△EBC∽△GBE,
∴![]() ,
,
∵BC=BD,
∴∠D=∠BCE,
∵∠BCE=∠DBE,
∴∠D=∠DBE,
∴BE=DE=![]() ,
,
∵∠AFE=∠ABD=90°,
∴BD∥EF,
∴∠D=∠CEF,
∴∠BCE=∠CEF,
∴CG=GE=3,
∴BC=BG+CG=BG+3,
∴![]() ,
,
∴BG=-8(舍)或BG=5,
即BG的长为5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.

(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
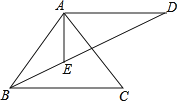
【题目】如图,AE、BE是△ABC的两个内角的平分线,过点A作AD⊥AE.交BE的延长线于点D.若AD=AB,BE:ED=1:2,则cos∠ABC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的一半
B.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的2倍
C.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半
D.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
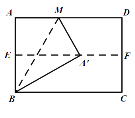
【题目】如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM,若矩形纸片的宽AB=4,则折痕BM的长为( )
A.![]() B.
B.![]() C.8D.
C.8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
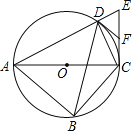
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
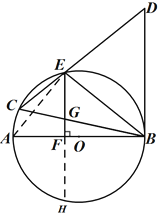
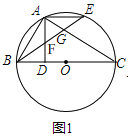
【题目】如图1,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,![]() ,BE分别交AD、AC于点F、G.
,BE分别交AD、AC于点F、G.
(1)判断△FAG的形状,并说明理由;
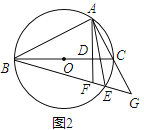
(2)如图2,若点E和点A在BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变,(1)中的结论还成立吗?请说明理由;
(3)在(2)的条件下,若BG=26,BD﹣DF=7,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 在
在![]() 和
和![]() 时的函数值相等.
时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数![]() 的图象与二次函数的图象都经过点A
的图象与二次函数的图象都经过点A![]() ,求m和k的值;
,求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移![]() 个单位后得到的图象记为C,同时将(2)中得到的直线
个单位后得到的图象记为C,同时将(2)中得到的直线![]() 向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com