练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    填空:已知,(如图)在△ABC中，BD为∠ABC的平分线，AB=BC，点P在BF上，PM⊥AD于M，PN⊥CD于N，求证：PM=PN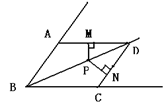

    证明：∵BD为∠ABC的平分线，∴∠ABD=∠CBD（               ）
    在△ABD和△CBD中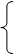
    AB=CB  (已知)
    ________________
    BD=BD  (公共边)
    ∴△ABD≌△CBD(       )
    ∴___________(                         )
    又∵________________________(已知)， ∴_____________.

    角平分线的定义，∠ABD=∠CBD，SAS，∠ADB=∠CDB，全等三角形的对应角相等，PM⊥AD   PN⊥CD，PM=PN。

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网在下面过程中的横线上填空．
    已知：如图，BC∥EF，BC=EF，AD=BE．求证：AC=DF．
    解：∵BC∥EF
    ∴∠ABC=∠
     

    又∵AD=BE（已知）
    ∴AB=
     

    在△ABC和△DEF中
     =  
     =  
     =  

    ∵
     
    =
     

     
    =
     

    ∴△ABC≌
     

    ∴
     
    =
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    22、结合图形填空：
    已知，如图，∠BAE+∠AED=180°，∠M=∠N
    试说明：∠1=∠2
    解：∵∠BAE+∠AED=180°
    ∴
    AB
    ∥
    CD
    （同旁内角互补，两直线平行）
    ∴∠BAE=
    ∠AEC
    （两直线平行，内错角相等）
    又∵∠M=∠N （已知）
    ∴
    AN
    ∥
    ME
    （内错角相等，两直线平行）
    ∴∠NAE=
    ∠MEA
    （两直线平行，内错角相等）
    ∴∠BAE-∠NAE=
    ∠AEC
    -
    ∠MEA

    即∠1=∠2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

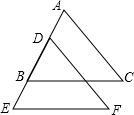
    根据题意填空：
    已知，如图，AD∥BC，∠BAD=∠BCD，求证：AB∥CD．
    证明：∵AD∥BC（已知）
    ∴∠1=
    ∠2（两直线平行，内错角相等），
    ∠2（两直线平行，内错角相等），

    又∵∠BAD=∠BCD （ 已知 ）
    ∴∠BAD-∠1=∠BCD-∠2
    （等式的性质）
    （等式的性质）

    即：∠3=∠4
    ∴
    AB∥CD（内错角相等，两直线平行）
    AB∥CD（内错角相等，两直线平行）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

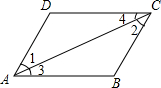
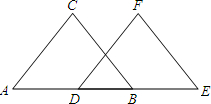    看图填空：
    已知：如图，BC∥EF，AD=BE，BC=EF，试说明 AC=DF
    解：∵AD=BE
    ∴AD+DB=BE+
    DB
    DB
    （等式的性质）
    即：AB=
    DE
    DE

    ∵BC∥EF
    ∴∠ABC=∠
    DEF
    DEF
    （
    两直线平行，同位角相等
    两直线平行，同位角相等
    ）
    在△ABC和△DEF中
    BC=EF (已知)
    (     )(已证)
    AB=DE (已证)

    ∴△ABC≌△DEF（
    SAS
    SAS
    ）
    ∴AC=DF （
    全等三角形的对应边相等
    全等三角形的对应边相等
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

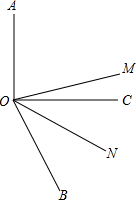    著名数学教育家G．波利亚，有句名言：“发现问题比解决问题更重要”，这句话启发我们：要想学好数学，就需要观察，发现问题，探索问题的规律性东西，要有一双敏锐的眼睛．请先观察、计算再填空．
    已知：如图，OM平分∠AOB，ON平分∠BOC．
    （1）当∠AOC=90°，∠BOC=70°时，∠MON=
    45°
    45°
    ；
    （2）当∠AOC=80°，∠BOC=60°时，∠MON=
    40°
    40°
    ；
    （3）当∠AOC=70°，∠BOC=50°时，∠MON=
    35°
    35°
    ；
    （4）猜想：不论∠AOC和∠BOC的度数是多少，∠MON的度数总等于
    ∠AOC
    ∠AOC
    度数的一半．

    查看答案和解析>>

    同步练习册答案