
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB、BC两部分组成,AB、BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为___________米(精确到1米,![]() ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).
,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() )的图象如图所示,对称轴为
)的图象如图所示,对称轴为![]() .有下列4个结论:①
.有下列4个结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 的增大而增大.其中,正确的结论有( )
的增大而增大.其中,正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,∠1=40°,∠2=80°,则∠3的度数为( )
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/15/2485292109684736/2491850430775296/STEM/0502255e02c3498e9234cb6eaef26eb9.png]
A.120°B.130°C.140°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
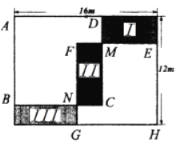
【题目】小明准备给长![]() 米,宽
米,宽![]() 米的长方形空地栽种花卉和草坪,图中I、II、III三个区域分别栽种甲、乙、丙三种花卉,其余区域栽种草坪.四边形
米的长方形空地栽种花卉和草坪,图中I、II、III三个区域分别栽种甲、乙、丙三种花卉,其余区域栽种草坪.四边形![]() 和
和![]() 均为正方形,且各有两边与长方形边重合;矩形
均为正方形,且各有两边与长方形边重合;矩形![]() (区域II)是这两个正方形的重叠部分,如图所示.
(区域II)是这两个正方形的重叠部分,如图所示.
(1)若花卉均价为![]() 元
元![]() ,种植花卉的面积为
,种植花卉的面积为![]()
![]() ,草坪均价为
,草坪均价为![]() 元
元![]() ,且花卉和草坪栽种总价不超过
,且花卉和草坪栽种总价不超过![]() 元,求
元,求![]() 的最大值.
的最大值.
(2)若矩形![]() 满足
满足![]() .
.
①求![]() ,
,![]() 的长.
的长.
②若甲、乙、丙三种花卉单价分别为![]() 元
元![]() ,
,![]() 元
元![]() ,
,![]() 元
元![]() ,且边
,且边![]() 的长不小于边
的长不小于边![]() 长的
长的![]() 倍.求图中I、II、III三个区域栽种花卉总价
倍.求图中I、II、III三个区域栽种花卉总价![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出![]() 的x的取值范围
的x的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
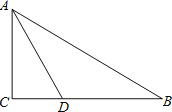
【题目】已知:如图,在![]() 中,
中,![]() 的角平分线
的角平分线![]() 交
交![]() 边于
边于![]() .
.
(1)以![]() 边上一点
边上一点![]() 为圆心,过
为圆心,过![]() 两点作
两点作![]() (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若(1)中的![]() 与
与![]() 边的另一个交点为
边的另一个交点为![]() ,
,![]() ,求线段
,求线段![]() 与劣弧
与劣弧![]() 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司接到一份新型高科技产品紧急订单,要求在![]() 天内(含
天内(含![]() 天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了该种产品
天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了该种产品![]() 件,以后每天生产的产品都比前一天多
件,以后每天生产的产品都比前一天多![]() 件.由于机器损耗等原因,当日生产的产品数量达到
件.由于机器损耗等原因,当日生产的产品数量达到![]() 件后,每多生产一件,当天生产的所有产品平均每件成本就增加
件后,每多生产一件,当天生产的所有产品平均每件成本就增加![]() 元.
元.
(1)设第![]() 天生产产品
天生产产品![]() 件,求出
件,求出![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
(2)若该产品每件生产成本(日生产量不超过![]() 件时)为
件时)为![]() 元,订购价格为每件
元,订购价格为每件![]() 元,设第
元,设第![]() 天的利润为
天的利润为![]() 元,试求
元,试求![]() 与
与![]() 之间的函数解析式,并求该公司哪一天获得的利润最大,最大利润的是多少?
之间的函数解析式,并求该公司哪一天获得的利润最大,最大利润的是多少?
(3)该公司当天的利润不低于![]() 元的是哪几天?请直接写出结果.
元的是哪几天?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
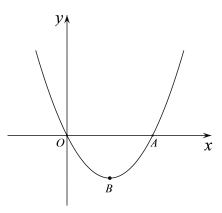
【题目】如图,抛物线y=x2+mx(m<0)交x轴于O,A两点,顶点为点B.
(1)求△AOB的面积(用含m的代数式表示);
(2)直线y=kx+b(k>0)过点B,且与抛物线交于另一点D(点D与点A不重合),交y轴于点C.过点C作CE∥AB交x轴于点E.
(ⅰ) 若∠OBA=90°,2<![]() <3,求k的取值范围;
<3,求k的取值范围;
(ⅱ) 求证:DE∥y轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
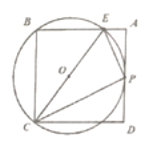
【题目】如图,已知在正方形![]() 中,
中,![]() ,
,![]() 是线段
是线段![]() 上的一动点,连接
上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .以
.以![]() 为直径作
为直径作![]() ,当点
,当点![]() 从点
从点![]() 移动到点
移动到点![]() 时,对应点
时,对应点![]() 也随之运动,则点
也随之运动,则点![]() 运动的路程长度为____________.
运动的路程长度为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com