
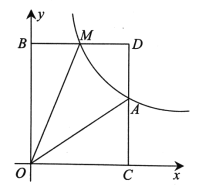
����Ŀ����֪����ͼ������������y=ax��ͼ���뷴��������![]() ��ͼ���ڵ�A��3,2����
��ͼ���ڵ�A��3,2����
��1���������������뷴���������ı���ʽ��
��2������ͼ��ֱ��д���ڵ�һ�����ڣ�![]() ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
��3��M��m��n���Ƿ���������ͼ���ϵ�һ�����㣬����0��m��3������M��ֱ��MB��x�ᣬ��y���ڵ�B������A��ֱ��AC��y�ύx���ڵ�C����ֱ��MB�ڵ�D�����ı���OADM�����Ϊ6ʱ��֤��BM=DM.
���𰸡���1����������������ʽΪy��![]() x����������������ʽΪ
x����������������ʽΪ![]() ��2��0��x��3��3��������
��2��0��x��3��3��������
��������
��1����A������ֱ��������������ʽ�����a��k��ֵ��������������Ľ���ʽ��
��2���ɷ�����������ͼ��������������ͼ����·�����ö�Ӧ��x��ȡֵ��Χ��
��3����M�������ɱ�ʾ����OCDB������͡�OBM��������Ӷ��ɱ�ʾ���ı���OADM��������ɵõ����̣������M������꣬�Ӷ���֤�����ۣ�
��1��������������y��ax��ͼ���뷴��������![]() ��ͼ���ڵ�A��3��2����
��ͼ���ڵ�A��3��2����
��2��3a��2��![]() �����a��
�����a��![]() ��k��6��
��k��6��
����������������ʽΪy��![]() x����������������ʽΪ
x����������������ʽΪ![]() ��
��
��2����ͼ���֪��������ͼ����ֱ��CD�����ʱ��������������ͼ��������������ͼ����Ϸ���
��A��3��2����
�൱0��x��3ʱ��������������ֵ����������������ֵ��
��3���������֪�ı���OCDBΪ���Σ�
��M��m��n����A��3��2����
��OB��n��BM��m��OC��3��AC��2��
��S����OCBD��OCOB��3n��S��OBM��![]() OBBM��
OBBM��![]() mn��S��OCA��
mn��S��OCA��![]() OCAC��3��
OCAC��3��
��S�ı���OADM��S����OCBDS��OBMS��OCA��3n![]() mn3��
mn3��
���ı���OADM�����Ϊ6ʱ������3n![]() mn3��6��
mn3��6��
�֡�M���ڷ���������ͼ���ϣ�
��mn��6��
��3n��12�����n��4����m��![]() ��
��
��BD��OA��3��
��MΪBD�е㣬
��BM��DM��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֲ���ڣ�ij��ѧ��֯ʦ����չֲ�����ֻ��Ϊ�˽�ȫУ800��ѧ����ֲ������������������50��ѧ����ֲ��������Ƴ�����ͳ�Ʊ�������ͳ��ͼ��
��1����![]() ��ֵ����������ͳ��ͼ����������
��ֵ����������ͳ��ͼ����������
��2�����50��ѧ���������ȡһ����ֲ������ǡ�õ�����λ���ĸ��ʣ�
��3�����Ƹ�У800��ѧ���У�ֲ������������4�õ�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪�����ڵ���ֱ���������У��ױ���һ��������Ϊ![]() ����ͼ1��
����ͼ1��![]() ��
��![]() ����
����![]() ��
��

֪ʶӦ�ã�
(1)��ͼ2��![]() ��
��![]() ��Ϊ����ֱ�������Σ�
��Ϊ����ֱ�������Σ�![]() ��
��![]() ��
��![]() ��
��![]() ���㹲�ߣ���
���㹲�ߣ���![]() ��
��![]() ����
����![]() �ij���
�ij���
֪ʶ���ӣ�
(2)��ͼ3��������![]() �У�
��![]() ��
��![]() ����
����![]() �Գƣ�
�Գƣ�![]() ��Ķ�Ӧ��Ϊ
��Ķ�Ӧ��Ϊ![]() �㣬
�㣬![]() ��
��![]() ���ӳ�����
���ӳ�����![]() �㣬����
�㣬����![]() ��
��
����֤��![]() ��
��
����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ�����4����С���ʵ���ȫ��ͬ��ƹ���������϶�����һ����С�ڣ�2��������֪����3��ƹ�����ϱ�����ֱ��ǣ�2��2��4�������4��������λ����0��
��1������4������������
��2��������ڴ����������1�����������������ϵ����������ĸ��ʣ�
��3��������ڴ����������1����(���Ż�)���ٴ����µ������������1�������б��������������������ϵ���֮��Ϊ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
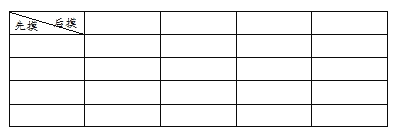
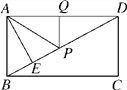
����Ŀ����ͼ���ھ���ABCD�У�AD��6��AE��BD������ΪE��DE��3BE����P��Q�ֱ���BD��AD �ϣ���AP��PQ����СֵΪ��
A. 2![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+��2��a��x��2��a��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C���������н��ۣ�
����a��0�������£�����aȡ��ֵ����A��һ�����㣻
����a��0�������£�����aȡ��ֵ�������ߵĶԳ���һ��λ��y�����ࣻ
��y����Сֵ�����ک�2��
����AB=AC����a=![]() ��
��
������ȷ�Ľ����У�����������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ����
����![]() ��
��![]() ��
��![]() ��
��
��1����������ߵĽ���ʽ��
��2������![]() �Ǹ������ߵ�����������һ�㣬���ı���
�Ǹ������ߵ�����������һ�㣬���ı���![]() ����������
����������
��3������![]() ��
��![]() ���ϣ���
���ϣ���![]() Ϊ�������ߵĶ��㣬��
Ϊ�������ߵĶ��㣬��![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020�����������ȫ���������۸��������ǣ������������������ĸ߶ȹ�ע���������г�Ͷ�봢����������˼۸�ƽ�֣���ͳ�ƣ�ij����2020��1��10������۸��ȥ��ͬһ��������40%������ó���ÿǧ������۸�Ϊ56Ԫ��

��1����2019��1��10�գ��ó�������ļ۸�Ϊÿǧ�˶���Ԫ��
��2������ij������ÿǧ��46Ԫ�ļ۸����⣬��2020��1��10�ռ۸���ۣ�ƽ��һ��������100ǧ��.�����������������ۼ�ÿǧ���½�1Ԫ��ƽ��ÿ��������������20ǧ�ˣ�����Ϊ��ʵ����������ƽ��ÿ����1120Ԫ�����������ھ����������ڹ˿͵�ǰ���£�ÿǧ������Ӧ�ö���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����ѧ�����Źܷ����������֪ʶ���˽��������400��ѧ���������֪ʶ���ԣ���������ǵijɼ����ٷ��ƣ���һ���Ǹ������ݻ��Ƶ�ͳ��ͼ����һ���֣�
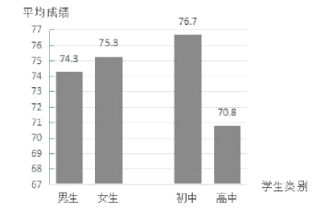
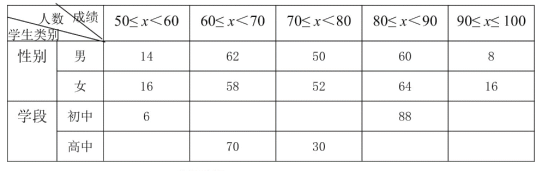
�������ĸ��ƶϣ�����400��ѧ�����Գɼ���ƽ����һ����74.3-75.3֮�䣻����400��ѧ�����Գɼ�����λ����70-80֮�䣻����400��ѧ���еij��������Գɼ�����λ��������60-70֮�䣻����400��ѧ���еĸ��������Գɼ�����λ��һ����60-70֮�䣻���к������ƶϵ������__________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com