
如下图,已知△ABC中,AB=10 cm,AC=8 cm,BC=6 cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2 cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
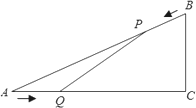
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
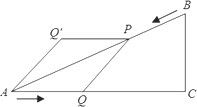
(4)如下图,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
|
分析:(1)由PQ∥BC时的比例线段关系,列一元一次方程求解; (2)如解答图1所示,过P点作PD⊥AC于点D,构造比例线段,求得PD,从而可以得到S的表达式,然后利用二次函数的极值求得S的最大值; (3)要点是利用(2)中求得的△AQP的面积表达式,再由线段PQ恰好把△ABC的面积平分,列出一元二次方程;由于此一元二次方程的判别式小于0,则可以得出结论:不存在这样的某时刻t,使线段PQ恰好把△ABC的面积平分; (4)首先根据菱形的性质及相似三角形比例线段关系,求得PQ、QD和PD的长度;然后在Rt△PQD中,求得时间t的值;最后求菱形的面积,值得注意的是菱形的面积等于△AQP面积的2倍,从而可以利用(2)中△AQP面积的表达式,这样可以化简计算. 解答:解:∵AB=10cm,AC=8cm,BC=6cm, ∴由勾股定理逆定理得△ABC为直角三角形,∠C为直角. (1)BP=2t,则AP=10-2t. ∵PQ∥BC,∴ ∴当t= (2)如图所示,过P点作PD⊥AC于点D.
∴PD∥BC,∴ S= ∴当t= (3)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分, 则有S△AQP= 由(2)可知,S△AQP=- ∴- ∵△=(-5)2-4×1×10=-15<0,此方程无解, ∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分. (4)假设存在时刻t,使四边形AQPQ′为菱形,则有AQ=PQ=BP=2t. 如图所示,过P点作PD⊥AC于点D,则有PD∥BC, ∴ 解得:PD=6- ∴QD=AD-AQ=8- 在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2, 即(8- 化简得:13t2-90t+125=0, 解得:t1=5,t2= ∵t=5s时,AQ=10cm>AC,不符合题意,舍去,∴t= 由(2)可知,S△AQP=- ∴S菱形AQPQ′=2S△AQP=2×(- 所以存在时刻t,使四边形AQPQ′为菱形,此时菱形的面积为
点评:本题是非常典型的动点型综合题,全面考查了相似三角形线段比例关系、菱形的性质、勾股定理及其逆定理、一元一次方程的解法、一元二次方程的解法与判别式、二次函数的极值等知识点,涉及的考点众多,计算量偏大,有一定的难度.本题考查知识点非常全面,是一道测试学生综合能力的好题. |
|
考点:相似三角形的判定与性质;一元二次方程的应用;二次函数的最值;勾股定理;勾股定理的逆定理;菱形的性质;翻折变换(折叠问题). |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
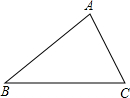 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com