
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法不正确的是( )

A.△ABE的面积=△BCE的面积B.∠AFG=∠AGF
C.BH=CHD.∠FAG=2∠ACF
【答案】C
【解析】
根据中线的性质即可判断A,根据直角三角形的锐角互余即可判断B,根据同角的余角相等以及角平分线的性质即可判断D.
根据三角形中线的性质可得:△ABE的面积和△BCE的面积相等,故A正确,
因为∠BAC=90°,所以∠AFG+∠ACF=90°,因为AD是高,所以∠DGC+∠DCG=90°,
因为CF是角平分线,所以∠ACF=∠DCG,所以∠AFG=∠DGC,又因为∠DGC=∠AGF,所以
∠AFG=∠AGF,故B正确,
因为∠FAG+∠ABC=90°,∠ACB+∠ABC=90°,所以∠FAG=∠ACB,又因为CF是角平分线,所以∠ACB=2∠ACF,所以∠FAG=2∠ACF,故D正确,
假设BH=CH,∠ACB=30°,则∠HBC=∠HCB=15°,∠ABC=60°,
所以∠ABE=60°-15°=45°,因为∠BAC=90°,所以AB=AE,因为AE=EC,所以![]() ,这与在直角三角形中30°所对直角边等于斜边的一半相矛盾,所以假设不成立,故④不一定正确,
,这与在直角三角形中30°所对直角边等于斜边的一半相矛盾,所以假设不成立,故④不一定正确,
故选A.


科目:初中数学 来源: 题型:
【题目】如图1,正方形MNPQ网格中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上.
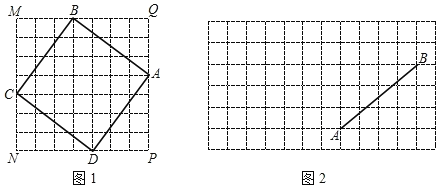
(1)设正方形MNPQ网格内的每个小方格的边长为1,求:正方形ABCD的面积;
(2)①在图2中画出以AB为一条直角边的等腰直角△ABC,且点C在小正方形的顶点上;
②在图2中画出以AB为一边的菱形ABDE,且点D和点E均在小正方形的顶点上,菱形ABDE的面积为15,连接CE,请直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
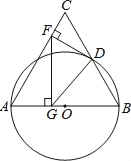
【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:
如图 1,AB∥CD,∠PAB=25°,∠PCD=37°,求∠APC的度数,小明的思路是:过点P作PE∥AB,通过平行线性质来求∠APC
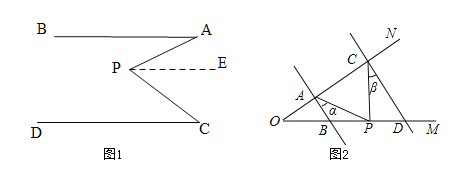
问题解决:
(1)按小明的思路,易求得∠APC 的度数为 °;
问题迁移:
如图 2,AB∥CD,点 P 在射线 OM 上运动,记∠PAB=α,∠PCD=β.
(2)当点 P 在 B,D 两点之间运动时,问∠APC 与α,β 之间有何数量关系? 请说明理由;
拓展延伸:
(3)在(2)的条件下,如果点 P 在 B,D 两点外侧运动时 (点 P 与点 O,B,D 三点不重合)请你直接写出当点 P 在线段 OB 上时,∠APC 与 α,β 之间的数量关系 ,点 P 在射线 DM 上时,∠APC 与 α,β 之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=1,AB>1,AG平分∠BAD,分别过点B,C作BE⊥AG 于点E,CF⊥AG于点F,则AE-GF的值为( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知:点A(0,0),B(![]() ,0),C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于( )
,0),C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com