
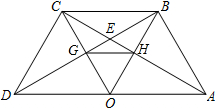
 如图,点O为线段AD上的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC,BD交于点E,AC,BD分别与OB,OC相交于点H,G,连接BC.
如图,点O为线段AD上的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC,BD交于点E,AC,BD分别与OB,OC相交于点H,G,连接BC.分析 (1)求出OC=OD,AB=OA,∠COD=∠OAB=60°,进而证得四边形AOCB是平行四边形,根据平行四边形的性质求得OH=BH,OG=CG,从而证得OH=OG,根据等边三角形的判定即可证得结论;
(2)求出OC=OD,OA=OB,∠DOB=∠COA,证△DOB≌△COA,推出∠DBO=∠CAO,在△BEA中,根据三角形内角和定理求出即可.
解答 (1)证明:∵△DCO和△ABO是等边三角形,
∴OC=OD,AB=OA,∠COD=∠OAB=60°,
∵OA=OD,
∴AB∥OC,OC=AB,
∴四边形AOCB是平行四边形,
∴OH=BH,
同理:OG=CG,
∴OH=OG,
∵∠COB=60°,
∴△OGH为等边三角形;
(2)解:∵△DCO和△ABO是等边三角形,
∴OC=OD,OB=OA,∠OBA=∠OAB=60°,∠COD=∠BOA=60°,
∴∠COD+∠COB=∠BOA+∠COB,
∴∠DOB=∠COA,
在△DOB和△COA中,
$\left\{\begin{array}{l}{OD=OC}\\{∠DOB=∠COA}\\{OB=OA}\end{array}\right.$
∴△DOB≌△COA(SAS),
∴∠DBO=∠CAO,
∵∠OBA=∠OAB=60°
∴∠AEB=180°-(∠EBO+∠OBA+∠BAO)
=180°-(∠CAO+∠OBA+∠BAO)
=180°-(60°+60°)=60°.
点评 本题考查了等边三角形性质,全等三角形的性质和判定,三角形的内角和定理的应用,关键是求出∠DBO=∠CAO.题目比较好.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
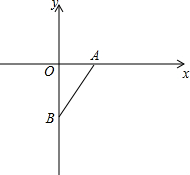 如图,已知平面直角坐标系中有点A(3,0)和点B(0,-4),在x轴上存在一点C,使得△ABC为等腰三角形,则C坐标为(-3,0)、(8,0)、(-2,0)、(-$\frac{7}{6}$,0).
如图,已知平面直角坐标系中有点A(3,0)和点B(0,-4),在x轴上存在一点C,使得△ABC为等腰三角形,则C坐标为(-3,0)、(8,0)、(-2,0)、(-$\frac{7}{6}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{54}$ | B. | $\frac{1}{26}$ | C. | $\frac{2}{27}$ | D. | $\frac{1}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com