Question

11．某市篮球队到市一中选拔一名队员．教练对王亮和李刚两名同学进行5次3分投篮测试，每人每次投10个球，如图记录的是这两名同学5次投篮中所投中的个数．

（1）请你根据图中的数据，填写表格；

姓名	平均数	众数	方差
王亮	7	7	0.4
李刚	7	7	2.8

（2）若你是教练，你打算选谁？简要说明理由．

Answer 1

分析 （1）根据平均数的定义，计算5次投篮成绩之和与5的商即为王亮每次投篮平均数；根据众数定义，李刚投篮出现次数最多的成绩即为其众数；先算出王亮的成绩的平均数，再根据方差公式计算王亮的投篮次数的方差．
（2）从平均数、众数、方差等不同角度分析，可得不同结果，关键是看参赛的需要

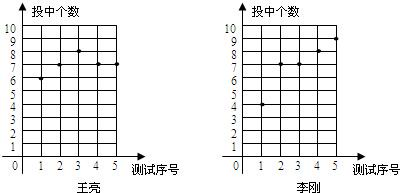
解答 解：（1）解：（1）李刚5次投篮，有2次投中7个，故7为众数；
王亮的方差为：S²=$\frac{1}{5}$（6-7）²+（7-7）²+…+（7-7）²]=0.4个
王亮投篮的平均数为：（6+7+8+7+7）÷5=7个，
故答案为7，0.4，7；
（2）两人的平均数、众数相同，从方差上看，王亮投篮成绩的方差小于李刚投篮成绩的方差．王亮的成绩较稳定．
选王亮的理由是成绩较稳定，选李刚的理由是他具有发展潜力，李刚越到后面投中数越多．

点评 此题是方差题，考查了实际问题，将数学知识与实际生活相联系，有利于培养学生学数学，用数学的意识，同时体现了数学来源于生活，应用于生活的本质．