
 如图所示,小岛P的周围20
如图所示,小岛P的周围20| 2 |
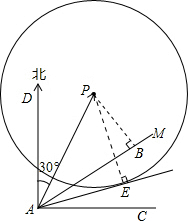 解:作PB⊥AM.
解:作PB⊥AM.| 2 |
20
| ||
| 40 |
| ||
| 2 |


科目:初中数学 来源: 题型:
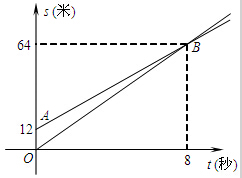 如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法:
如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点C和点D在线段AB上,AE∥BF,AE=FB,AC=DB,连接EC、ED、FC、FD.
如图,点C和点D在线段AB上,AE∥BF,AE=FB,AC=DB,连接EC、ED、FC、FD.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:
如图:| 2 |
| p |
| q |
| p |
| q |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
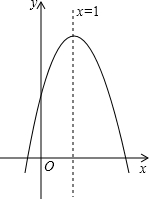 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的个数是( )| A、4个 | B、3个 | C、2个 | D、1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积是多少?
如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com