练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】△ABC在直角坐标系内的位置如图所示．

    （1）请直接写出A、B、C的坐标；

    （2）请在这个坐标系内画出△A1B1C1，使△A1B1C1与△ABC关于y轴对称，并写出B1的坐标；

    （3）计算△A1B1C1面积．

    【答案】（1）A（0，3）；B（-4，4）；C（-2，1）；（2）B1（4，4），见详解；（3）5

    【解析】

    （1）观察平面直角坐标系，根据点与坐标系的关系，即可求得A、B、C的坐标；
    （2）根据关于y轴对称的图形的特点，首先求得各对称点的坐标，继而画出△A1B1C1；

    （3）利用割补法求解可得．

    解：（1）A（0，3）；B（-4，4）；C（-2，1）；

    （2）如图：B1的坐标为：（4，4）；

    （3）△A1B1C1的面积为4×3-×2×2-×2×3-×1×4=5．

    故答案为：（1）A（0，3）；B（-4，4）；C（-2，1）；（2）B1（4，4），见详解；（3）5

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1＝∠2，则下列条件中，不能使△ABC≌△DBC成立的是　（　　）

    A. AB＝CD B. AC＝BD C. ∠A＝∠D D. ∠ABC＝∠DCB

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠C=Rt∠，AC=8cm，BC=6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒2cm，设运动的时间为t秒。

    (1)当t为何值时，CP把△ABC的周长分成相等的两部分。

    (2)当t为何值时，CP把△ABC的面积分成相等的两部分，并求出此时CP的长；

    (3)当t为何值时，△BCP为等腰三角形?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一种实验用轨道弹珠，在轨道上行驶5分钟后离开轨道，前2分钟其速度v（米/分）与时间t（分）满足二次函数v=at2，后三分钟其速度v（米/分）与时间t（分）满足反比例函数关系，如图，轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分，求：

    （1）二次函数和反比例函数的关系式．

    （2）弹珠在轨道上行驶的最大速度．

    【答案】（1）v=（2＜t≤5） （2）8米/分

    【解析】分析：（1）由图象可知前一分钟过点（1，2），后三分钟时过点（2，8），分别利用待定系数法可求得函数解析式；

    （2）把t=2代入（1）中二次函数解析式即可．

    详解：（1）v=at2的图象经过点（1，2），

    ∴a=2．

    ∴二次函数的解析式为：v=2t2，（0≤t≤2）；

    设反比例函数的解析式为v=，

    由题意知，图象经过点（2，8），

    ∴k=16，

    ∴反比例函数的解析式为v=（2＜t≤5）；

    （2）∵二次函数v=2t2，（0≤t≤2）的图象开口向上，对称轴为y轴，

    ∴弹珠在轨道上行驶的最大速度在2秒末，为8米/分．

    点睛：本题考查了反比例函数和二次函数的应用．解题的关键是从图中得到关键性的信息：自变量的取值范围和图象所经过的点的坐标．

    【题型】解答题
    【结束】
    24

    【题目】阅读材料：小胖同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来则形成一组旋转全等的三角形．小胖把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小胖发现若∠BAC=∠DAE，AB=AC，AD=AE，则BD=CE．

    （1）在图1中证明小胖的发现；

    借助小胖同学总结规律，构造“手拉手”图形来解答下面的问题：

    （2）如图2，AB=BC，∠ABC=∠BDC=60°，求证：AD+CD=BD；

    （3）如图3，在△ABC中，AB=AC，∠BAC=m°，点E为△ABC外一点，点D为BC中点，∠EBC=∠ACF，ED⊥FD，求∠EAF的度数（用含有m的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在学校开展的数学活动课上，小明和小刚制作了一个正三楼锥（质量均匀，四个面完全相同），并在各个面上分别标记数字1，2，3，4，游戏规则如下每人投掷三棱锥两次，并记录底面的数字，如果两次所掷数字的和为单数，那么算小明赢，如果两欢所掷数字的和为偶数，那么算小明赢；

    （1）请用列表或者面树状围的方法表示上述游戏中的所有可能结果．

    （2）请分别隶出小明和小刚能赢的概率，并判新游戏的公平性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点C.抛物线经过A，C两点，且与x轴交于另一点B（点B在点A右侧）．

    （1）求抛物线的解析式及点B坐标；

    （2）若点M是线段BC上的一动点，过点M的直线EF平行y轴交x轴于点F，交抛物线于点E.求ME长的最大值；

    （3）试探究当ME取最大值时，在抛物线上、x轴下方是否存在点P，使以M，F，B，P为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

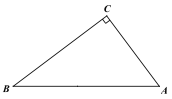
    【题目】如图，Rt△ABC，AC⊥CB,AC=15，AB=25,点D为斜边上动点。

    （1）如图，过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时，求CE；

    （2）如图，在点D的运动过程中，连接CD，若△ACD为等腰三角形，求AD。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：

    材料一：两个含有二次根式的非零代数式相乘，如果它们的积不含二次根式，那么这两个代数式互为有理化因式.

    例如：，我们称的一个有理化因式是的一个有理化因式是.

    材料二：如果一个代数式的分母中含有二次根式，通常可将分子、分母同乘分母的有理化因式，使分母中不含根号，这种变形叫做分母有理化.

    例如：，

    请你仿照材料中的方法探索并解决下列问题：

    (1)的有理化因式为______，的有理化因式为______.(均写出一个即可)

    (2)将下列各式分母有理化(要求写出变形过程)：

    ①.

    ②.

    (3)请从下列A，B两题中任选一题作答，我选择题.

    A计算：的结果为______.

    B计算：的结果为_____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知港口A东偏南10°方向有一处小岛B，一艘货轮从港口A沿南偏东40°航线出发，行驶80海里到达C处，此时观测小岛B在北偏东60°方向．

    （1）求此时货轮到小岛B的距离．

    （2）在小岛周围36海里范围内是暗礁区，此时轮船向正东方向航行有没有触礁危险？请作出判断并说明理由．

    查看答案和解析>>

    同步练习册答案