
分析 分类讨论::(1)当x-1≥0时,原方程化为x2-x=0,(2)当x-1<0时,原方程化为x2+x-2=0,然后利用因式分解法分别解两个一元二次方程,再利用x的范围确定原方程的解.
解答 解:(1)当x-1≥0时,即x≥1 时,原方程化为x2-x=0,
x(x-1)=0,
解得x1=0(舍去),x2=1;
(2)当x-1<0时,即x<1时,原方程化为x2+x-2=0,
(x+2)(x-1)=0,
解得x1=1(舍去),x2=-2,
所以原方程的解为x=1或-2.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 矩形的对角线互相平分且相等 | |
| B. | 等腰三角形底边上的中点到两腰的距离相等 | |
| C. | 等腰梯形的两条对角线相等 | |
| D. | 对角线互相垂直的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
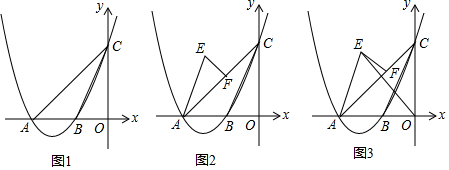
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
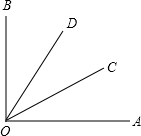 如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.
如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
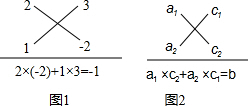
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com