
分析 (1)根据已知条件可得b=-(a+c),a>-(a+c)>c,两边同时除以a即可求解;
(2)先求得方程ax2+2bx+c=0根的判别式为4[(a+$\frac{1}{2}$c)2+$\frac{3}{4}$c2],根据非负数的性质和已知条件可得△>0,先令x1>x2,通过证明x1<2即可求解.
解答 (1)解:a>b>c,a+b+c=0,
b=-(a+c),
a>-(a+c)>c,
-2<$\frac{c}{a}$<-$\frac{1}{2}$;
(2)证明:△=(2b)2-4ac
=4b2-4ac=4(a+c)2-4ac
=4(a2+c2+ac)
=4[(a+$\frac{1}{2}$c)2+$\frac{3}{4}$c2]≥0,
且a≠c≠0,
∴△>0,
∴有两个不相等的实根,
解方程ax2+2bx+c=0得x=$\frac{-b±\sqrt{{b}^{2}-ac}}{a}$,
令x1>x2,
x1=$\frac{-b+\sqrt{{b}^{2}-ac}}{a}$=$\frac{a+c+\sqrt{{a}^{2}+{c}^{2}+ac}}{a}$=1+$\frac{c}{a}$+$\sqrt{1+\frac{{c}^{2}}{{a}^{2}}+\frac{c}{a}}$,
∵-2<$\frac{c}{a}$<-$\frac{1}{2}$,
∴x1=1+$\frac{c}{a}$+$\sqrt{(\frac{c}{a}+\frac{1}{2})^{2}+\frac{3}{4}}$<2,
∴方程ax2+2bx+c=0有两个不相等的实根,且均小于2.
点评 考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.


科目:初中数学 来源: 题型:解答题
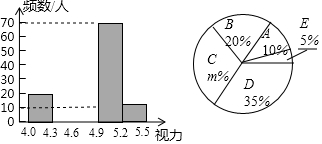 某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.| 组别 | 视力 | 频数(人) |
| A | 4.0≤x<4.3 | 20 |
| B | 4.3≤x<4.6 | a |
| C | 4.6≤x<4.9 | b |
| D | 4.9≤x<5.2 | 70 |
| E | 5.2≤x<5.5 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
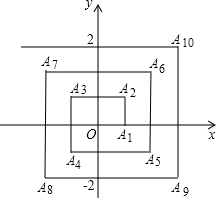 如图,已知A1(1,0),A2(-1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…则点A2017的坐标为(505,-504).
如图,已知A1(1,0),A2(-1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…则点A2017的坐标为(505,-504).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
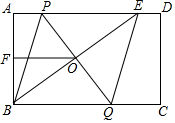 如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{(x+1)^{2}}$=x+1 | D. | $\sqrt{-4x}$=$\sqrt{-4}\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
| A. | x与y都是变量,且x是自变量,y是x的函数 | |
| B. | 弹簧不挂重物时的长度为0cm | |
| C. | 物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 所挂物体质量为7kg时,弹簧长度为23.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com