
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
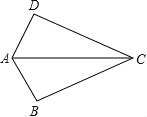
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
【答案】C
【解析】
试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-![]() .
.
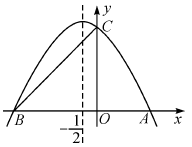
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 对全国中学生心理健康现状的调查 B. 对神舟飞船发射前零部件的调查
C. 对我市市民实施低碳生活情况的调查 D. 对市场上的冰淇淋质量的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与直线交于
与直线交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() 点坐标为(1,0).
点坐标为(1,0).
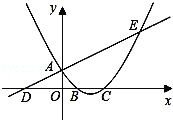
(1)求该抛物线的解析式;
(2)动点![]() 在
在![]() 轴上移动,当△
轴上移动,当△![]() 是直角三角形时,直接写出点
是直角三角形时,直接写出点![]() 的坐标;
的坐标;
(3)在抛物线的对称轴上找一点![]() ,使|
,使|![]() |的值最大,求出点
|的值最大,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料瓶上有这样的字样:Eatable Date 18 months.如果用x(单位:月)表示Eatable Date(保质期),那么该饮料的保质期可以用不等式表示为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】次函数的图象与x轴、y轴分别交于点A(8,0)和点B(0,6).
(1)确定此一次函数的解析式.
(2)求坐标原点O到直线AB的距离.
(3)点P是线段AB上的一个动点,过点P作PM垂直于x轴于M,作PN垂直于y轴于N,记L=PM+PN,问L是否存在最大值和最小值?若存在,求出此时P点到原点O的距离,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com