
【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.
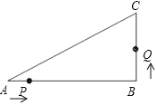
(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
【答案】(1)![]() cm;(2)在运动过程中,△PQB能形成等腰三角形,出发后
cm;(2)在运动过程中,△PQB能形成等腰三角形,出发后![]() 秒后第一次形成等腰三角形.(3)4.
秒后第一次形成等腰三角形.(3)4.
【解析】
试题分析:(1)求出AP、BP、BQ,根据勾股定理求出PQ即可.
(2)根据等腰直角三角形得出BP=BQ,代入得出方程,求出方程的解即可.
(3)根据周长相等得出10+t+(6-2t)=8-t+2t,求出即可.
试题解析:
(1)∵出发2秒后AP=2cm,
∴BP=8-2=6(cm),
BQ=2×2=4(cm),
在Rt△PQB中,由勾股定理得:![]() (cm)
(cm)
即出发2秒后,求PQ的长为![]() cm
cm
(2)在运动过程中,△PQB能形成等腰三角形,
AP=t,BP=AB-AP=8-t;BQ=2t
由PB=BQ得:8-t=2t
解得t=![]() (秒),
(秒),
即出发后![]() 秒后第一次形成等腰三角形.
秒后第一次形成等腰三角形.
(3)Rt△ABC中由勾股定理得:![]() (cm);
(cm);
∵AP=t,BP=AB-AP=8-t,BQ=2t,QC=6-2t,
又∵线段PQ第一次把直角三角形周长分成相等的两部分,
∴由周长相等得:AC+AP+QC=PB+BQ
10+t+(6-2t)=8-t+2t
解得t=4(cm)
即从出发4秒后,线段PQ第一次把直角三角形周长分成相等的两部分.


科目:初中数学 来源: 题型:
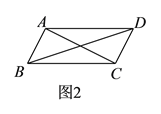
【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= ______ °时,四边形BECD是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,平行四边形
,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .将直线
.将直线![]() 绕点
绕点![]() 顺时针旋转分别交
顺时针旋转分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.

(![]() )在旋转过程中,线段
)在旋转过程中,线段![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(![]() )如图
)如图![]() ,若
,若![]() ,当旋转角至少为__________
,当旋转角至少为__________![]() 时,四边形
时,四边形![]() 是平行四边形,并证明此时的四边形是
是平行四边形,并证明此时的四边形是![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:

①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中:
①当x>0时,y>0;
②若a=﹣1,则b=4;
③抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2;正确的是( )
A.①
B.②
C.③
D.①②③都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C,E,F在直线AB的同侧时(如图①所示),试说明∠BOE=2∠COF.
(2)当点C与点E,F在直线AB的两侧时(如图②所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级(1)班体育委员统计了全班同学60秒跳绳次数,并列出了下面的不完整频数分布表和不完整的频数分布直方图.根据图表中的信息解答问题
组别 | 跳绳次数 | 频数 |
A | 60≤x<80 | 2 |
B | 80≤x<100 | 6 |
C | 100≤x<120 | 18 |
D | 120≤x<140 | 12 |
E | 140≤x<160 | a |
F | 160≤x<180 | 3 |
G | 180≤x<200 | 1 |
合计 | 50 | |
(1)求a的值;
(2)求跳绳次数x在120≤x<180范围内的学生的人数;
(3)补全频数分布直方图,并指出组距与组数分别是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com