
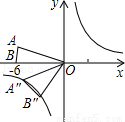
��13�֣���ͼ��������OAB��ֱ������ϵ�е�λ����ͼ����A������Ϊ��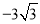 ��3������B������Ϊ��-6��0��.
��3������B��������-6��0��.
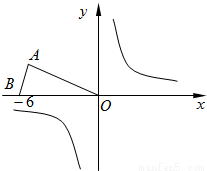
��1������OAB����y�����Գ�ͼ����������OA��B�䣬��ֱ��д��A��B�ĶԳƵ�A�䡢B������ꣻ
��2������������OAB��x������ƽ��a����λ����ʱ��Aǡ�����ڷ���������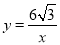 ��ͼ���ϣ���a��ֵ��
��ͼ���ϣ���a��ֵ��
��3������OAB�Ƶ�O����ʱ�뷽����ת���ȣ�0������90����
�ٵ���=30��ʱ��Bǡ�����ڷ���������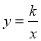 ��ͼ���ϣ���k��ֵ��
��ͼ���ϣ���k��ֵ��
���ʵ�A��B�ܷ�ͬʱ���ڢ��еķ�����������ͼ���ϣ����ܣ��������ֵ�������ܣ���˵�����ɣ�
��1�����ڡ�OAB����y�����Գ�ͼ���ǡ�OA'B'������A��A�����y��Գƣ�B��B�����y��Գƣ���֪����A������Ϊ��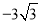 ��3������B������Ϊ����6��0�����ʣ�A�䣨
��3������B������Ϊ����6��0�����ʣ�A�䣨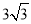 ��3����B'��6��0����
��3����B'��6��0����
��2�����Aƽ�ƺ�����˫����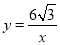 ��ʱ������ΪA�䣨m��n������A��
��ʱ������ΪA�䣨m��n������A��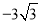 ��3��������֪��n=3��
��3��������֪��n=3��
����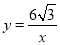 �����m��
�����m��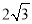 ����ƽ�Ƶľ���a��|
����ƽ�Ƶľ���a��|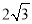 ����
����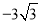 ��|��
��|��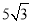 ��
��
��3����B����������ǣ���6sin������6��sin30�㣽��3���������ǣ���6cos������6cos30�㣽��3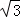 ��B��������ǣ���
��B��������ǣ���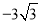 ����3����k��
����3����k��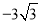 ������3����
������3����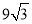 ��
��
�ڡߵ�A����Ϊ��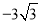 ��3������OA��6����OA��OB��6����tan��AOB��
��3������OA��6����OA��OB��6����tan��AOB��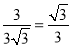 �����AOB=30�㣬����BOA�壽30��ʱ�����BOB�壽60�㣬A�������Ϊ��
�����AOB=30�㣬����BOA�壽30��ʱ�����BOB�壽60�㣬A�������Ϊ��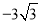 ����3����B�������Ϊ����3��
����3����B�������Ϊ����3�� �������ʱ��A��B��ͬʱ���ڢ��еķ�����������ͼ���ϣ�ͬ��������240��Ҳ�������⣻�����60���240�㣮
�������ʱ��A��B��ͬʱ���ڢ��еķ�����������ͼ���ϣ�ͬ��������240��Ҳ�������⣻�����60���240�㣮
��������
��1������OAB����OA��B�����y��Գƣ���ôA��A���Լ�B��B�䶼����y��Գƣ��ɾݴ˵õ�A�䡢B������ꣻ��2�����ݵ�A����Ϊ��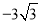 ��3��������OAB��x������ƽ��a����λ����ʱ��Aǡ�����ڷ���������
��3��������OAB��x������ƽ��a����λ����ʱ��Aǡ�����ڷ���������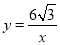 ��ͼ���ϣ���ƽ���Ժ�����������3����y=3�������ʽ�Ϳ��Եõ�A��ƽ�ƺ�ĵ�ĺ����꣬�õ�a��ֵ����3�� ��OAB�Ƶ�O����ʱ�뷽����ת30�ȣ��Ϳ��������ת�������꣬���뷴��������
��ͼ���ϣ���ƽ���Ժ�����������3����y=3�������ʽ�Ϳ��Եõ�A��ƽ�ƺ�ĵ�ĺ����꣬�õ�a��ֵ����3�� ��OAB�Ƶ�O����ʱ�뷽����ת30�ȣ��Ϳ��������ת�������꣬���뷴��������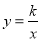 �Ľ���ʽ���Ϳ������k��ֵ��
�Ľ���ʽ���Ϳ������k��ֵ��
���㣺��ת�����ʣ�����ϵ����������������ʽ��


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭���˻���ׯ����У���꼶��ѧ��12���¿���ѧ�Ծ��������棩 ���ͣ�������
2������3��������5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����а��꼶��ѧ����ĩ��ѧ�Ծ��������棩 ���ͣ������
��ͳ�ƣ�2012��2013�������ݺ����������Ʊ�����ܶ�Ϊ579600000Ԫ����ң���ȷ������λ�ɱ�ʾΪ_________Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶1���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
�ڣ�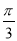 ��0.3030030003������ÿ������3֮���1��0������
��0.3030030003������ÿ������3֮���1��0������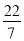 ��3.14��
��3.14�� 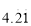 ���������� �� ��
���������� �� ��
A��2�� B��3�� C��4�� D��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶1���¿���ѧ�Ծ��������棩 ���ͣ������
��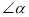 �������38��24�䣬��
�������38��24�䣬��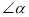 �IJ���Ϊ �㣮
�IJ���Ϊ �㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ӱ�ʡ�����о��꼶��ѧ�ڵ������¿���ѧ�Ծ��������棩 ���ͣ������
��10�֣���ͼ���ڵ�λ����Ϊ1�������������У�һ��Բ����������Ľ���A��B��C��
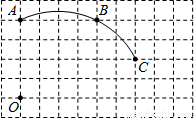
��1����������²�����
���Ե�OΪԭ�㡢��ֱ��ˮƽ�������ڵ�ֱ��Ϊ�����ᡢ����߳�Ϊ��λ��������ƽ��ֱ������ϵ������ֱ�ߺ�Բ�滭����Բ������Բ��Բ��D��λ�ã�����д������������ͼ�ۼ�����������AD��CD��
��2�����ڣ�1���Ļ����ϣ�����������⣺
��д��������꣺C ��D ��
�ڡ�D�İ뾶= .�� ����������ţ���
��������ADC��һ��Բ�IJ���չ��ͼ�����Բ�ĵ������. ����������У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ӱ�ʡ�����о��꼶��ѧ�ڵ������¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
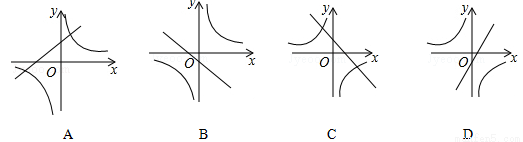
��ͬһƽ��ֱ������ϵ�У�����y=kx+k��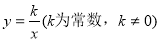 ��ͼ������ǣ� ��
��ͼ������ǣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ӱ�ʡ�����о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��10�֣���֪����x�ķ���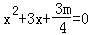 ��
��
��1������˷�������������ȵ�ʵ��������m��ȡֵ��Χ��
��2���ڣ�1���У���mΪ����������������������ʱ���̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ���꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
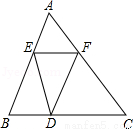
��ͼ��ʾ����ABC�У�E��F��D�ֱ��DZ�AB��AC��BC�ϵĵ㣬������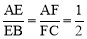 �����EFD���ABC�������Ϊ( )
�����EFD���ABC�������Ϊ( )
A.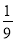 B.
B.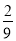 C.
C.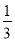 D.
D.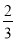
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com