
分析 根据二次根式有意义的条件得:被开方数为非负数,则a(x-a)≥0,x-a≥0,a(y-a)≥0,a-y≥0,所以a=0,先将a=0代入已知得:x=-y,最后再代入所求式子即可.
解答 解:∵a(x-a)≥0,x-a≥0,
∴a≥0,
∵a(y-a)≥0,a-y≥0,
∴a≤0,
∴a=0,
把a=0代入已知条件中得:$\sqrt{x}$-$\sqrt{-y}$=0,
x=-y,
则x+y=0,
∴$\frac{x+y}{x-y}$=0.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.本题先根据二次根式有意义的条件得到字母的值或关系,然后代入所求的式子进行计算.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.
如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
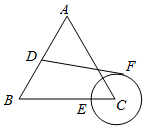 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )| A. | 有最大值,无最小值 | B. | 有最小值,无最大值 | ||
| C. | 有最大值,也有最小值 | D. | 为定值 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2最大 | B. | a最大 | C. | b最大 | D. | c最大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com