
 如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( )
如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | 2$\sqrt{5}$ |
分析 首先利用勾股定理计算出BD的长,进而得到BO的长,在直角三角形CDN中,根据勾股定理求出DN,即得出BN,在直角三角形BON中,用勾股定理求出ON即可.
解答 解:如图,连接BM,DN
在矩形纸片ABCD中,CD=AB=2,∠C=90°,
在Rt△BCD中,BC=4,
根据勾股定理得,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=2$\sqrt{5}$,
∴OB=$\frac{1}{2}$BD=$\sqrt{5}$,
由折叠得,∠BON=90°,ON=$\frac{1}{2}$MN,BN=DN,
∵BC=BN+CN=4,
∴CN=4-BN,
在Rt△CDN中,CD=2,
根据勾股定理得,CN2+CD2=DN2,
(4-BN)2+22=BN2,
∴BN=$\frac{5}{2}$,
在Rt△BON中,ON=$\sqrt{B{N}^{2}-B{O}^{2}}$=$\frac{\sqrt{5}}{2}$,
∴MN=2ON=$\sqrt{5}$,
故选B.
点评 此题主要考查了图形的翻折变换和勾股定理,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解此类题目常用的方法是构造直角三角形.


科目:初中数学 来源: 题型:选择题
| A. | 100(1+x%)2=64 | B. | 100(1-x%)2=64 | C. | 100(1-x)2=64 | D. | 100[(1-(x%)2]=64 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC的周长为36cm,DE垂直平分边AC,交BC边于点E,交AC边于点D,连接AE,若AD=$\frac{15}{2}$cm,则△ABE的周长是( )
如图,△ABC的周长为36cm,DE垂直平分边AC,交BC边于点E,交AC边于点D,连接AE,若AD=$\frac{15}{2}$cm,则△ABE的周长是( )| A. | 22cm | B. | 20 cm | C. | 21cm | D. | 15cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=3cm,则AB的长度为( )
如图,Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=3cm,则AB的长度为( )| A. | 6cm | B. | 9cm | C. | 12cm | D. | 15cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出以下结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}_{1}+{x}_{2}+{x}_{3}}{3}$ | B. | $\frac{a{x}_{1}+b{x}_{2}+c{x}_{3}}{a+b+c}$ | ||
| C. | $\frac{a{x}_{1}+b{x}_{2}+c{x}_{3}}{3}$ | D. | $\frac{a+b+c}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:判断题
已知,A,B 两市相距 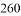 千米,甲车从 A 市前往 B 市运送物资,行驶
千米,甲车从 A 市前往 B 市运送物资,行驶  小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过
小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过  分钟修好甲车后以原速原路返回,同时甲车以原速
分钟修好甲车后以原速原路返回,同时甲车以原速 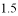 倍的速度前往 B 市,如图是两车距 A 市的路程
倍的速度前往 B 市,如图是两车距 A 市的路程  (千米)与甲车行驶时间
(千米)与甲车行驶时间  (小时)之间的函数图象,结合图象回答下列问题:
(小时)之间的函数图象,结合图象回答下列问题:
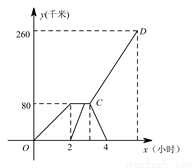
(1)直接写出甲车提速后的速度、乙车的速度、点  的坐标;
的坐标;
(2)求乙车返回时  与
与  的函数关系式并直接写出自变量
的函数关系式并直接写出自变量  的取值范围;
的取值范围;
(3)求甲车到达 B 市时乙车已返回 A 市多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com