
分析 (1)由题意得出第x档次提高的档次是x-1档,根据总利润=单件利润×产量可得函数解析式;
(2)根据题意列出关于x的一元二次方程,解方程求得x的值,结合x的范围取舍即可得;
(3)将函数解析式配方成顶点式即可得最值情况.
解答 解:(1)∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天生产量减少5件.
∴第x档次,提高的档次是x-1档.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)由题意可得:-10x2+180x+400=1120
整理得:x2-18x+72=0
解得:x1=6,x2=12(舍去).
答:该产品的质量档次为第6档.
(3)∵y=-10x2+180x+400=-10(x-9)2+1210
∴该产品一天的总利润为y的最大值=1210元.
点评 本题主要考查二次函数的应用和一元二次方程的应用,根据相等关系列出函数解析式及一元二次方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b2>4c | B. | x1+x2>m+n | C. | x1x2>mn | D. | m<x1<x2<n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
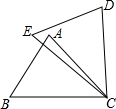 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )| A. | ∠BCE=∠ACD | B. | AC=DC | C. | ∠A=∠D | D. | AB=DE |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{6}}{3}$ | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
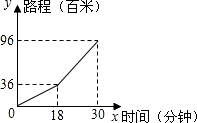 小明早晨从进学校骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度和原来相同,那么小亮从学校骑车回家用的时间是37.2分钟.
小明早晨从进学校骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度和原来相同,那么小亮从学校骑车回家用的时间是37.2分钟.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com