练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，已知△ABC内接于⊙O，CD是⊙O的切线与半径OB的延长线交于点D，∠A=30°，求∠BCD的度数．

    分析 如图，连接OC． 构建直角△OCD和等边△OBC，结合图形，可以得到∠BCD=90°-∠OCB=30°．

    解答 解：如图，连接OC．
    ∵CD是⊙O的切线，
    ∴∠OCD=90°．
    ∵∠A=30°，
    ∴∴∠COB=2∠=60°．
    ∵OC=OB，
    ∴△OBC是等边三角形，
    ∴∠OCB=60°，
    ∴∠BCD=90°-∠OCB=30°．

    点评 本题考查了切线的性质和圆周角定理．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

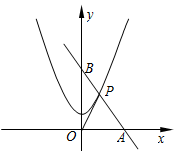    4．已知，如图，直线AB经过点B（0，6），且tan∠ABO=$\frac{2}{3}$，与抛物线y=ax2+2在第一象限内相交于点P，又知△AOP的面积为6．
    （1）求a的值；   
    （2）能否将抛物线y=ax2+2平移使得平移后的抛物线经过点A？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

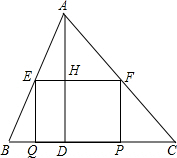    5．如图所示，在△ABC中，BC=10，高AD=8，矩形=EFPQ的一边QP在BC边上，E、F两点分别在AB、AC上，AD交EF于点H．
    （1）求证：$\frac{AH}{AD}$=$\frac{EF}{BC}$；
    （2）设EF=x，当x为何值时，矩形EFPQ的面积最大？并求其最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．三角形两边长为4和11，第三边长为3-6m，则m的取值范围是（　　）
    A．-2＜m＜-$\frac{2}{3}$B．m＞-2C．-2≤m≤-$\frac{2}{3}$D．m＜-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．列一元一次方程解应用题．
    某租赁公司拥有100辆轿车，当每辆轿车的月租金为3000元时，可全部租出，当每辆轿车的月租金每增加50元时，未租出的轿车将会增加一辆，租出的轿车每辆每月公司需要保养费150元，未租出的轿车每辆每月公司需要保养费50元．
    （1）已知10月份每辆轿车的月租金为3600元时，能租出多少辆轿车？
    （2）已知11月份的保养费开支为12900元，问该月租出了多少辆轿车？
    （3）比较10、11两月的月收益，哪个月的月收益多？多多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．某中学要组织一次篮球比赛，赛制为单循环形式（毎两队之间都赛一场），计划安排21场比赛，求参加的球队支数，如果设参加的球队支数为x，则可列方程为（　　）
    A．$\frac{1}{2}$x（x+1）=21B．x（x+1）=21C．$\frac{1}{2}$x（x-1）=21D．x（x-1）=21

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图所示，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D，要使四边形OACB为菱形，还需要添加一个条件，这个条件可以是②或③或④．
    ①AD=BD
    ②OD=CD
    ③∠OAD=∠DAC
    ④∠OAD=∠ABC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

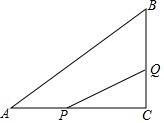    3．如图，在△ABC中，∠C=90°，AC=8cm，BC=6cm，点P沿AC边从点A以1cm/s的速度向终点C运动，同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动
    （1）当点Q在CB边上运动时，点P、Q出发几秒后，△PCQ的面积为12cm2；
    （2）当点Q在CB边上运动时，点P、Q出发几秒后，△PCQ与△ACP相似；
    （3）求整个运动过程中，△APQ的面积S与运动时间t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．在围棋盒中有x颗白色棋子和y颗黑色棋子，从盒中随机取出一颗棋子，取得白色棋子的概率是$\frac{1}{3}$，如再往盒中放进4颗黑色棋子，取得白色棋子的概率变为$\frac{1}{5}$，则x2+y2=20．

    查看答案和解析>>

    同步练习册答案