
【题目】问题提出
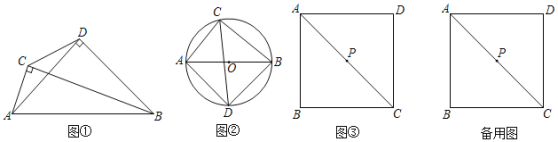
(1)如图1.已知∠ACB=∠ADB=90°,请用尺规作图作出△ABD的外接圆(保留作图痕迹,不写作法);点C是否在△ABD的外接圆上 (填“是”或“否”).
问题探究
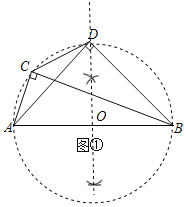
(2)如图2.四边形ADBC是⊙O的内接四边形,∠ACB=∠ADB=90°,AD=BD.求证:CA+CB=![]() CD;
CD;
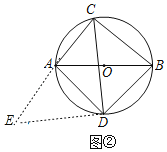
(3)如图3.点P是正方形ABCD对角线AC的中点,点E是平面上一点,EB=AB且EA=![]() BA.点Q是线段AE的中点,请在图中画出点E,并求线段PQ与AB之间的数量关系.
BA.点Q是线段AE的中点,请在图中画出点E,并求线段PQ与AB之间的数量关系.
【答案】问题提出(1)作△ABD的外接圆,见解析;是;问题探究(2)见解析;(3)画出点E,见解析; PQ=![]() AB,PQ=
AB,PQ=![]() AB.
AB.
【解析】
(1)作AB的垂直平分线交AB于点O,以O为圆心,AO长为半径作圆,即为△ABD的外接圆,利用四点共圆的性质可说明C在圆上;
(2)如图2,作辅助线,把AC+BC转化为CE,可证得△CDE是等腰直角三角形,从而右证明结论成立;
(3)以点B为圆心,AB长为半径作圆,以点A为圆心,![]() AB长为半径作圆,两圆的交点为E,注意有两个交点都符合题意;连接BQ,BP,设AB=3x,在Rt
AB长为半径作圆,两圆的交点为E,注意有两个交点都符合题意;连接BQ,BP,设AB=3x,在Rt![]() 中求得
中求得![]() ,易证得AQBP四点共圆且AP=BP,AP⊥BP,运用(2)的结论可求得PQ的值,继而求得线段PQ与AB之间的数量关系.
,易证得AQBP四点共圆且AP=BP,AP⊥BP,运用(2)的结论可求得PQ的值,继而求得线段PQ与AB之间的数量关系.
问题提出
(1)作AB的垂直平分线交AB于点O,以O为圆心,AO长为半径作圆,即为△ABD的外接圆,
∵∠ACB=∠ADB=90°,
∴点A,点B,点D,点C四点共圆,
∴点C在△ABD的外接圆上,
故答案为:是;
问题探究
(2)如图2,将△BCD绕点D,逆时针旋转90°到△AED处,
∴∠EAD=∠DBC,
∵四边形ADBC是圆内接四边形,
∴∠DBC+∠DAC=180°,
∴∠EAD+∠DAC=180°,
∴E、A、C三点共线,
∴∠CAE为平角,
由旋转知,AE=BC,DE=CD,∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CE=![]() CD,
CD,
∵CE=AE+AC=BC+AC,
∴CA+CB=![]() CD;
CD;
(3)如图3,连接BQ,BP,
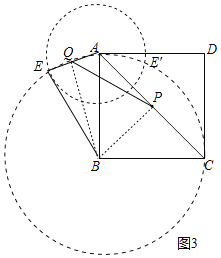
∵以点B为圆心,AB长为半径作圆,以点A为圆心,![]() AB长为半径作圆,两圆的交点为E,
AB长为半径作圆,两圆的交点为E,
∴点A的左右各有个点E,
设AB=3x,则AE=x,
若点E在点A的左侧,
∵BE=AB,点Q是AE的中点,
∴BQ⊥AE,AQ=EQ=![]() ,
,
∴BQ=![]() ,
,
∵四边形ABCD是正方形,点P是对角线AC的中点,
∴AP=BP,AP⊥BP,
由(2)的结论可得:AQ+BQ=![]() PQ,
PQ,
∴![]() PQ=
PQ=![]()
∴PQ=![]() ,
,
∴PQ=![]() ,
,
若点E在点A的右侧,
同理可求:PQ=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB=AC,D是优弧BC上的一个动点,连结AD交BC于点E,连结BD.
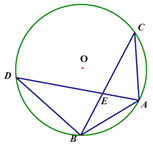
(1)若AE=2,DE=8,求AC的长;
(2)若D是优弧BC上中点时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
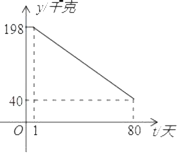
【题目】荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:![]() (1≤t≤80,t为整数),日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1≤t≤80,t为整数),日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
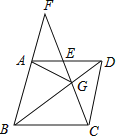
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.
查看答案和解析>>
科目:初中数学 来源: 题型:
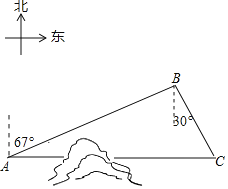
【题目】如图,C地在A地的正东方向,因有大山阻隔.由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地130km,C地位于B地南偏东30°方向.若打通穿山隧道.建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中对 600 名毕业生中考体育测试坐位体前屈成绩进行整理,绘制成 如下不完整的统计图:
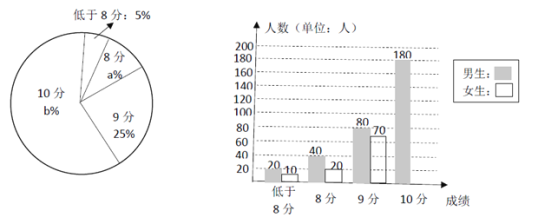
根据统计图,回答下列问题。
(1)请将条形统计图补充完整;
(2)扇形统计图中,b= ,得 8 分所对应扇形的圆心角度数为 ;
(3)在本次调查的学生中,随机抽取 1 名男生,他的成绩不低于 9 分的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸是一家水果店的经理.一天,他去水果批发市场,用100元购进甲种水果,用100元购进乙种水果,已知乙种水果比甲种水果多10千克,乙种水果的批发价比甲种水果的批发价低0.5元.
(1)求甲、乙两种水果各购进了多少千克?
(2)如果当天甲、乙两种水果都按2.80元出售,乙种水果很快售完,而甲种水果先售出![]() ,剩余的按售价打5折售完.请你通过计算,说明这一天的水果买卖是否赚钱?如果赚钱,赚了多少元?如果不赚钱,那么赔了多少元?
,剩余的按售价打5折售完.请你通过计算,说明这一天的水果买卖是否赚钱?如果赚钱,赚了多少元?如果不赚钱,那么赔了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com