
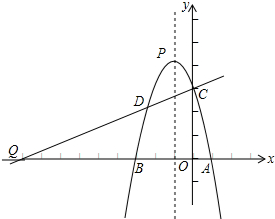
 如图,已知抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3),抛物线的顶点为P,连结AC.
如图,已知抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3),抛物线的顶点为P,连结AC.分析 (1)运用待定系数法即可得到解析式;
(2)利用△QOC∽△COA,得出QO的长度,得出Q点的坐标,再求出直线QC的解析式,将两函数联立求出交点坐标即可.
解答 (1)设此抛物线的解析式为:y=a(x-x1)(x-x2)
∵抛物线与x轴交于A(1,0)、B(-3,0)两点,
∴y=a(x-1)(x+3)
∵抛物线与y轴交于点C(0,3)
∴a(0-1)(0+3)=3,
∴a=-1
∴y=-(x-1)(x+3)
即y=-x2-2x+3;
(2)∵点A(1,0),点C(0,3)
∴OA=1,OC=3,
∵DC⊥AC,OC⊥x轴
∴△QOC∽△COA
∴$\frac{OQ}{OC}=\frac{OC}{OA}$,即$\frac{OQ}{3}=\frac{3}{1}$
∴OQ=9,
∵点Q在x轴的负半轴上,
∴Q(-9,0)
设直线DC的解析式为:y=kx+b,则$\left\{\begin{array}{l}b=3\\-9k+b=0\end{array}\right.$解之得:$\left\{\begin{array}{l}k=\frac{1}{3}\\ b=3\end{array}\right.$
∴直线DC的解析式为:$y=\frac{1}{3}x+3$
∵点D是抛物线与直线DC的交点,
∴$\left\{\begin{array}{l}y=\frac{1}{3}x+3\\ y=-{x^2}-2x+3\end{array}\right.$解之得:$\left\{\begin{array}{l}{x_1}=-\frac{7}{3}\\ y{\;}_1=\frac{20}{9}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=0}\\{{y}_{2}=3}\end{array}\right.$(不合题意,舍去)
∴点D$(-\frac{7}{3},\frac{20}{9})$.
点评 此题主要考查了二次函数的综合应用,特别注意利用数形结合是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
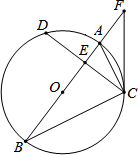 如图,在⊙O中,直径AB平分弦CD、AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB平分弦CD、AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com