
(12分)如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.
(1)求证:△CEB≌△ADC;
 (2)若AD=9cm,DE=6cm,求BE及EF的长.
(2)若AD=9cm,DE=6cm,求BE及EF的长.
证明:(1)∵B E⊥C E于E,AD⊥CE于D,
∴∠E=∠ADC=90°(1分)
∠BCE=90°— ∠ACD,∠CAD=90°¾∠ACD,
∴∠BCE=∠CAD (3分)
在△BCE与△CAD 中,
∠E=∠ADC,∠BCE=∠CAD, BC = AC ∴△C E B≌△AD C (4分)
(2)∵△C E B≌△AD C ∴ B E= D C, C E= AD
又AD=9 ∴C E= AD=9,D C= C E — D E= 9—6 = 3,∴B E= DC =3( cm) (5分)
∵∠E=∠ADF=90°,∠B FE=∠AFD,∴△B FE∽△ AFD (6分)
∴![]() 即有
即有 ![]() (7分)
(7分)
解得:EF=![]() ( cm) (8分)
( cm) (8分)
解析:略


科目:初中数学 来源: 题型:
(本题12分)如图,已知抛物线y=![]() x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y= x+b相交于点B、C,直线y=
x+b相交于点B、C,直线y=![]() x+b与y轴交于点E.
x+b与y轴交于点E.
(1)写出直线BC的解析式;
(2)求△ABC的面积;
(3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A、B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒,请写出△MNB的面积s与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分12分)如图,已知一次函数y=kx+b的图象交反比例函数
![]() 的图象于点A、B,交x轴于点C.
的图象于点A、B,交x轴于点C.
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且![]() =
=![]() ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
 轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为 .
轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为 .查看答案和解析>>
科目:初中数学 来源:2013届江苏省宿迁市四校(修远、青华中学)九年级第二次联考数学试卷(带解析) 题型:解答题
(本题满分12分)
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.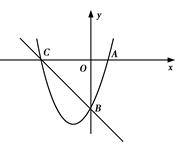
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年山东省初中毕业入学摸底考试数学试卷 题型:解答题
(本小题满分12分)如图,已知一次函数y=kx+b的图象交反比例函数
 的图象于点A、B,交x轴于点C.
的图象于点A、B,交x轴于点C.
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且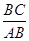 =
= ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com