
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
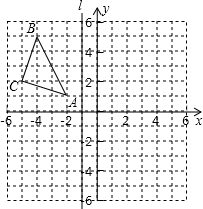 如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2),直线l经过点(-1,0)且和y轴平行.
如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2),直线l经过点(-1,0)且和y轴平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交$\widehat{BC}$于D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交$\widehat{BC}$于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM运动,当他运动2米到达点D处时,测得影长DN=0.6m,再前进2米到达点B处时,测得影长MB=1.6m,(图中线段AB、CD、EF表示小明的身高)
如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM运动,当他运动2米到达点D处时,测得影长DN=0.6m,再前进2米到达点B处时,测得影长MB=1.6m,(图中线段AB、CD、EF表示小明的身高)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com