
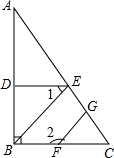
 如图,已知DE⊥AB,BC⊥AB,∠1+∠2=180°,判断BE与FG是否平行,并说明理由.
如图,已知DE⊥AB,BC⊥AB,∠1+∠2=180°,判断BE与FG是否平行,并说明理由.科目:初中数学 来源: 题型:
 如图所示,A、B关于y轴对称的两点,点P(2,3)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.
如图所示,A、B关于y轴对称的两点,点P(2,3)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A、B两建筑物位于河的两岸,要测得它们之间的距离,可以从B点出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E、C、A在同一直线上,则DE的长就是A、B之间的距离,请你说明道理,你还能想出其他方法吗?
如图,A、B两建筑物位于河的两岸,要测得它们之间的距离,可以从B点出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E、C、A在同一直线上,则DE的长就是A、B之间的距离,请你说明道理,你还能想出其他方法吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com