科目：初中数学 来源：初中数学 三点一测丛书 八年级数学 下 （江苏版课标本） 江苏版 题型：044
阅读下面的解题过程，然后解答后面的问题．
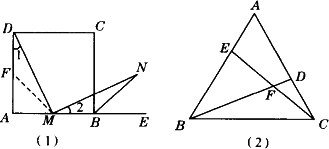
题目：如图(1)，已知正方形ABCD中，点M是AB的中点，点E是AB延长线上的一点，MN⊥DM交∠CBE的平分线BN于点N．试说明MD＝MN．
解：在AD上取一点F，使AF＝AM，连结MF．
因为ABCD是正方形，
所以DF＝MB，∠1＋∠AMD＝90°．
因为DM⊥MN，
所以∠AMD＋∠2＝90°．
所以∠1＝∠2．
因为BN平分∠CBE，
所以∠MBN＝135°＝∠DFM．
所以△DFM≌△MBN．
所以DM＝MN．
(1)在上述说理过程中，“点M是AB的中点”这个条件没有用到，若将这个条件改为“点M是AB上的任意一点”，或“点M是AB延长线上的任意一点”，或“点M是BA延长线上的任意一点”，则结论“DM＝MN”还成立吗？请说明理由；
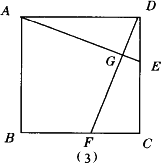
(2)如图(2)，在正三角形ABC中，若AE＝CD，则∠BFE＝60°；如图(3)，在正方形ABCD中，若DE＝CF，则∠AGF＝90°．这里的两个结论“∠BFE＝60°”和“∠AGF＝90，分别与题目的背景条件“正三角形ABC”和“正方形ABCD”有关．你能否改编一道题目，改变上述题目的背景“正方形ABCD”，并相应改变条件“MN⊥DM”，而其余条件与结论不变？请说明所编题目的正确性．
查看答案和解析>>
科目：初中数学 来源：2008年四川省攀枝花市初中毕业升学统一考试、数学试卷 题型：044
先阅读下列材料，再解答后面的问题
材料：一般地，n个相同的因数a相乘：
．如23＝8，此时，3叫做以2为底8的对数，记为log28(即log28＝3)．一般地，若an＝b(a＞0且a≠1，b＞0)，则n叫做以a为底b的对数，记为logab(即logab＝n)．如34＝81，则4叫做以3为底81的对数，记为log381(即log381＝4)．
问题：(1)计算以下各对数的值：
log24＝________ log216＝________ log264＝________．
(2)观察(1)中三数4、16、64之间满足怎样的关系式？log24、log216、log264之间又满足怎样的关系式？
(3)由(2)的结果，你能归纳出一个一般性的结论吗？
logaM＋logaN＝________(a＞0且a≠1，M＞0，N＞0)
根据幂的运算法则：an·am＝an+m以及对数的含义证明上述结论．
查看答案和解析>>
科目：初中数学 来源：2011届河北省蠡县中考模拟考试数学试卷（带解析） 题型：解答题
如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE绕A点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM＝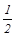
BD，EN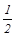＝CE，得到图③，请解答下列问题：
(1)若AB＝AC，请探究下列数量关系：
①在图②中，BD与CE的数量关系是________________；
②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；
(2)若AB＝k·AC(k＞1)，按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN与∠BAC的数量关系，直接写出你的猜想，不必证明．
查看答案和解析>>
科目：初中数学 来源：2010-2011学年河北省蠡县中考模拟考试数学试卷（解析版） 题型：解答题
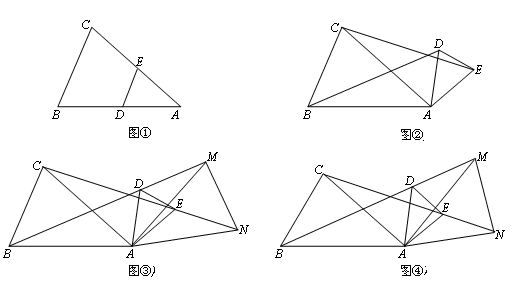
如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE绕A点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM＝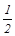
BD，EN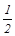＝CE，得到图③，请解答下列问题：
(1)若AB＝AC，请探究下列数量关系：
①在图②中，BD与CE的数量关系是________________；
②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；
(2)若AB＝k·AC(k＞1)，按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN与∠BAC的数量关系，直接写出你的猜想，不必证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
;②
