
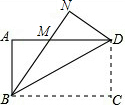
 如图,把一张矩形的纸沿对角线折叠,若AB=4cm,BM=5cm,则△BMD的面积S=10cm2.
如图,把一张矩形的纸沿对角线折叠,若AB=4cm,BM=5cm,则△BMD的面积S=10cm2. 分析 由折叠的性质得出∠MBD=∠CBD,由矩形的性质得出∠MDB=∠CBD,得出∠MBD=∠MDB,由等角对等边得出DM=BM=5cm,△BMD的面积=$\frac{1}{2}$DM•AB,即可得出结果.
解答 解:由折叠的性质得:∠MBD=∠CBD,
∵四边形ABCD是矩形,
∴AD∥BC,∴∠MDB=∠CBD,
∴∠MBD=∠MDB,
∴DM=BM=5cm,
∴△BMD的面积=$\frac{1}{2}$DM•AB=$\frac{1}{2}$×5×4=10(cm2);
故答案为:10.
点评 本题考查了翻折变换的性质、矩形的性质、等腰三角形的判定、三角形面积的计算;熟练掌握翻折变换和矩形的性质,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
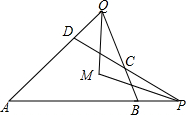 如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.
如图,已知,四边形ABCD,P,Q在AB、AD的延长线上,PM,QM分别平分∠APC和∠AQC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
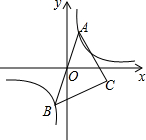 如图,已知点A是双曲线y=$\frac{1}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-1.
如图,已知点A是双曲线y=$\frac{1}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
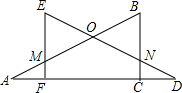 两块含30°角的全等直角三角形木板,按如图所示方式摆放,使得两条相等的直角边AC,DF在同一条直线上.此时MF与NC是否相等?请说明理由.
两块含30°角的全等直角三角形木板,按如图所示方式摆放,使得两条相等的直角边AC,DF在同一条直线上.此时MF与NC是否相等?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com