
 如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.在AB边上有一个动点F,且不与点A,B重合.当AF=$\frac{16}{11}$时,△MEF的周长最小.
如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.在AB边上有一个动点F,且不与点A,B重合.当AF=$\frac{16}{11}$时,△MEF的周长最小. 分析 如图1,做点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,由(1)可得AM,利用勾股定理可得ME和NM′,由△AFM′∽△NEM′,利用相似三角形的性质可得AF;
解答 解:∵四边形ABCD为矩形,
∴CD=AB=4,∠D=90°,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴PD=PH=3,CD=MH=4,∠H=∠D=90°,
∴PM=5,
如图1,做点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,
∵AM=AD-MP-PD=12-5-3=4,
∴AM=AM′=4,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,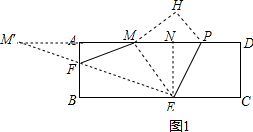
∴∠CEP=∠MEP,∠CEP=∠MPE,
∴∠MEP=∠MPE,
∴ME=MP=5;
在Rt△ENM中,MN=3,
∴NM′=11,
∵AF∥ME,
∴△AFM′∽△NEM′,
∴$\frac{M′A}{M′N}$=$\frac{AF}{EN}$,
即$\frac{4}{11}$=$\frac{AF}{4}$,
解得:AF=$\frac{16}{11}$,
即AF=$\frac{16}{11}$时,△MEF的周长最小;
故答案为:$\frac{16}{11}$.
点评 本题主要考查了折叠的性质和最短路径问题,做对称点利用勾股定理是解答此题的关键.


科目:初中数学 来源: 题型:解答题
 甲、乙两车从A地出发匀速行驶至B地,在整个行驶过程中,甲、乙两车离开A地的距离y1(单位:km),y2(单位:km)关于甲车行驶的时间t(单位:h)的函数关系如图所示,根据图象解答下列问题:
甲、乙两车从A地出发匀速行驶至B地,在整个行驶过程中,甲、乙两车离开A地的距离y1(单位:km),y2(单位:km)关于甲车行驶的时间t(单位:h)的函数关系如图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.
如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是40cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com