
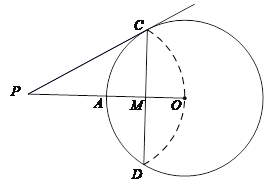
【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
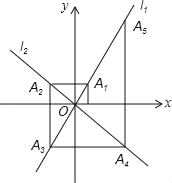
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1…过点A1作y轴的垂线交L2于点A2,过点A2作x轴的垂线交于点A3,过点A3作y轴的垂线交L2于点A4,依次进行下去,则点A2018的坐标为( )
A. (﹣21009,21009) B. (﹣21009,﹣21010)
C. (﹣1009,1009) D. (﹣1009,﹣2018)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
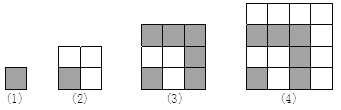
【题目】用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
 …
…
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有25小正方形;
……
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n-1)的结果(用含n的代数式表示);
(2)请根据你的发现计算:① 1+3+5+7+…+99;
② 101+103+105+…+199.
查看答案和解析>>
科目:初中数学 来源: 题型:
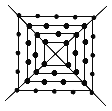
【题目】如图,有一个形如四边形的点阵,第1层每边有2个点,第2层每边有3个点,第3层每边有4个点,依此类推.
(1)第10层共有 个点,第n层共有 个点;
(2)如果某一层共有96个点,它是第几层?
(3)有没有一层点数为150个点,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
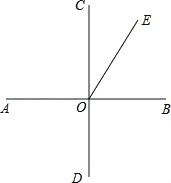
【题目】如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°)
(1)比较∠AOD,∠EOB,∠AOE大小(用“<”连接)
(2)如∠EOC=28°,求∠EOB和∠EOD的度数(适当写出解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com