
【题目】阅读材料:
关于三角函数还有如下的公式:
sin(α±β)=sin αcos β±cos αsin β
tan(α±β)= ![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan 15°=tan(45°-30°)=  =2-
=2-![]() .
.
根据以上阅读材料,请选择适当的公式解答下面问题:
(1)计算sin 15°的值.
(2)乌蒙铁塔是六盘水市标志性建筑物之一,小华想用所学的知识来测量该铁塔的高度.如图,小华站在离铁塔底A距离7 m的C处,测得铁塔顶B的仰角为75°,小华的眼睛离地面的距离DC为1.62 m,请帮助小华求出乌蒙铁塔的高度.(结果精确到0.1 m.参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
![]()
【答案】(1)![]() ;(2)27.7m.
;(2)27.7m.
【解析】试题分析:(1)把15°化为45°-30°以后,再利用公式![]() 计算,即可求出
计算,即可求出![]() 的值;
的值;
(2)先根据锐角三角函数的定义求出![]() 的长,再根据
的长,再根据![]() 即可得出结论.
即可得出结论.
试题解析:(1)sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°·sin 30°=![]() .
.
(2)在Rt△BDE中, ![]() tan∠BDE=
tan∠BDE=![]() ,
,
![]() BE=DE·tan∠BDE=7tan75°(m),
BE=DE·tan∠BDE=7tan75°(m),
![]() AB=AE+BE=1.62+7×
AB=AE+BE=1.62+7×![]() ,
,
=1.62+7×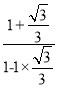 =1.62+7×
=1.62+7×![]() =1.62+7×(2+
=1.62+7×(2+![]() ),
),
≈1.62+7×(2+1.732),
=1.62+26.124=27.744≈27.7(m),
即乌蒙铁塔的高度约为27.7 m.


科目:初中数学 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
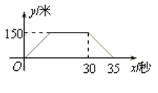
【题目】火车匀速通过隧道时,火车在隧道内的长度![]() (米)与火车行驶时间
(米)与火车行驶时间![]() (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
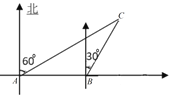
【题目】如图,某货船以24海里/时的速度将一批重要物资从![]() 处运往正东方向的M处,在点
处运往正东方向的M处,在点![]() 处测得某岛
处测得某岛![]() 在北偏东
在北偏东![]() 的方向上.该货船航行
的方向上.该货船航行![]() 分钟后到达
分钟后到达![]() 处,此时再测得该岛在北偏东
处,此时再测得该岛在北偏东![]() 的方向上,已知在
的方向上,已知在![]() 岛周围
岛周围![]() 海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,P是边AB上的一点,连接CP.
(1)要使△ACP∽△ABC,还需要补充的一个条件是_____.
(2)若△ACP∽△ABC,且AC=![]() ,AB=3,求AP的长.
,AB=3,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP:PQ:QR.

查看答案和解析>>
科目:初中数学 来源: 题型:
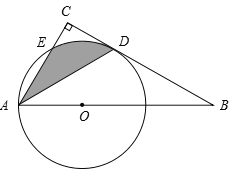
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC相切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留π![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com