
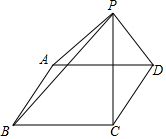
 如图,平行四边形ABCD的两个高分别为3cm和4cm,P为平行四边形ABCD外一点,三角形PBC的面积为20cm2,三角形PAD的面积为8cm2,求平行四边形ABCD的周长?
如图,平行四边形ABCD的两个高分别为3cm和4cm,P为平行四边形ABCD外一点,三角形PBC的面积为20cm2,三角形PAD的面积为8cm2,求平行四边形ABCD的周长? 分析 如图,作PM⊥BC于M交AD于N.由S△PBC-S△PAD=12,推出$\frac{1}{2}$•BC•PM-$\frac{1}{2}$•AD•PN=12,因为AD=BC,MN=3或4,BC=8或6,由BC•3=AB•4=24,或BC•4=AB•3=24,由此即可解决问题.
解答 解:如图,作PM⊥BC于M交AD于N.
∵S△PBC-S△PAD=12,
∴$\frac{1}{2}$•BC•PM-$\frac{1}{2}$•AD•PN=12,
∵AD=BC,MN=3或4,
∴BC•MN=24,
∴BC=8或6,
∵BC•3=AB•4=24,或BC•4=AB•3=24,
∴AB=6或8,
∴平行四边形ABCD的周长为28.
点评 本题考查平行四边形的性质、三角形的面积、平行四边形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会利用面积法求线段的长,属于中考常考题型.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:选择题
 如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )| A. | (1,0) | B. | (-1,0) | C. | (-1,1) | D. | (1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:
我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点到达终点后,另外一点也随之停止运动.
已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点到达终点后,另外一点也随之停止运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com