
【题目】已知:在![]() 中,
中, ![]() ,
, ![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),且
重合),且![]() .
.
(![]() )如图
)如图![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() __________
__________![]() ,
, ![]() __________
__________![]() .
.
(![]() )如图
)如图![]() ,①求证:
,①求证: ![]() .
.
②若![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.


【答案】(1)![]() ,
, ![]() ;(2)①见解析;②
;(2)①见解析;②![]()
【解析】试题分析:(1)由等腰三角形的性质得到∠EBC=∠ECB=27°,根据角平分线的性质得到∠DEB=∠EBC+∠ECB=54°,再由角平分线的性质得到∠ACD=∠ECB=27°,因为∠EAC=2∠EBC=54°,求得∠AEC=180°-27°-54°=99°;
(2)在CB上截取CF,使CF=CA,连接EF,构造全等三角形,由全等三角形的性质推出AE=FE,再根据FB=FE,得到AE=FB,即可得出AE+AC=FB+FC=BC;
(3)在CB上截取CF,使CF=CA,连接EF,连接AF,由∠ECB=30°,得到∠ACB=60°,于是推出△AFC是等边三角形,通过三角形全等得到∠EBC=∠FAE,由∠FAC=60°,得到∠EAC=2∠EBC=2∠FAE,于是得出∠EBC的度数.
试题解析:解:(1)∵EB=EC,∴∠EBC=∠ECB=27°,∴∠DEB=∠EBC+∠ECB=54°.
∵CD平分∠ACB,∴∠ACD=∠ECB=27°.
∵∠EAC=2∠EBC=54°,∴∠AEC=180°-27°-54°=99°.
故答案为:54°,99°.
(2)①证明:如图1,在BC上取一点M,使BM=ME,∴∠MBE=∠MEB.
∵∠EAC=2∠MBE,∠EMC=∠MBE+∠MEB=2∠MBE,∴∠EAC=∠EMC.
在△ACE与△MCE中,∵∠CAE=∠CME,∠ACE=∠MCE,CE=CE,∴△ACE≌△MCE(AAS),∴AE=ME, AC =CM,∴AE=BM,∴BC=BM+CM=AE+AC.
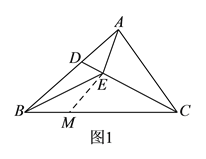
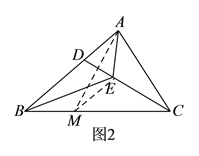
②如图2在BC上取一点M,使BM=ME,连接AM.
∵∠ECB=30°,∴∠ACB=60°,由①可知,△AMC是等边三角形(M点与B点重合),∴AM=AC=BE.
在△EMB与△MEA中,∵AE=BM,EM=EM,AM=BE,∴△EMB≌△MEA,∴∠EBC=∠MAE.
∵∠MAC=60°,∠EAC=2∠EBC=2∠MAE,∴∠MAE=20°,∠EAC=40°,∴∠EBC=20°.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】化简,求值
(1)5x2y+{xy﹣[5x2y﹣(7xy2+![]() xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣
xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣![]() ,y=﹣16.
,y=﹣16.
(2)A=4x2﹣2xy+4y2,B=3x2﹣6xy+3y2,且|x|=3,y2=16,|x+y|=1,求4A+[(2A﹣B)﹣3(A+B)]的值.
(3)如果m﹣3n+4=0,求:(m﹣3n)2+7m3﹣3(2m3n﹣m2n﹣1)+3(m3+2m3n﹣m2n+n)﹣m﹣10m3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 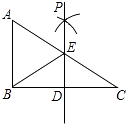
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.
(1)求该函数的解析式,并画出它的图象;
(2)如果这条直线经过点P(m,2),求m的值;
(3)若O为坐标原点,求直线OP的解析式;
(4)求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
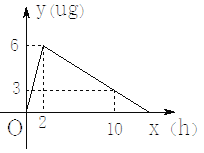
【题目】某医药研究生开发了一种新药,在实验药效时发现,如果成人按规剂量服用,那么服用药后2h时血液中含药量最高,达每毫升6ug,接着逐步衰减,10h时血液中含药量每毫升3ug,每毫升血液中含药量y(ug)随时间x(h)的变化如图所示,当成人按规定剂量服药后.
(1)分别求出x≤2和x>2时,y与x之间的函数关系式;
(2)如果每毫升血液含药量为4ug或4ug以上时在治疗疾病时是有效的,那么这个有效时间是多长?每天至少吃几次药疗效最好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保证学生有足够的睡眠,政协委员于今年两会向大会提出一个议案,即“推迟中小学生早晨上课时间”,这个议案当即得到不少人大代表的支持.根据北京市教委的要求,学生小强所在学校将学生到校时间推迟半小时.小强原来7点从家出发乘坐公共汽车,7点20分到校;现在小强若由父母开车送其上学,7点45分出发,7点50分就到学校了.已知小强乘自家车比乘公交车平均每小时快36千米,求从小强家到学校的路程是多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题:
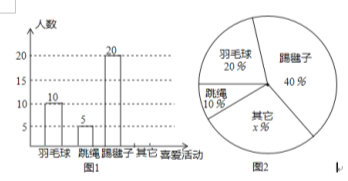
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据 ②图2中x= .
(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.
(1)试求抛物线的解析式;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,∠ACB=30°,AB=5,△ABC的面积为23.
(1)若点P在AB边上且CP=![]() ,D,E分别为边AC,BC上的动点.求△PDE周长的最小值;
,D,E分别为边AC,BC上的动点.求△PDE周长的最小值;
(2)假设一只小羊在△ABC区域内,从路边AB某点出发跑到水沟边AC喝水,然后跑向路边BC吃草,再跑回出发点处休息,直接写出小羊所跑的最短路程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com