【题目】如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=500，∠C=600，求∠DAE和∠BOA的度数。
【答案】
解：∵∠A=50°，∠C=60°
∴∠ABC=180°-50°-60°=70°，
又∵AD是高，
∴∠ADC=90°，
∴∠DAC=180°-90°-∠C=30°，
∵AE、BF是角平分线，
∴∠CBF=∠ABF=35°，∠EAF=25°，
∴∠DAE=∠DAC-∠EAF=5°，
∠AFB=∠C+∠CBF=60°+35°=95°，
∴∠BOA=∠EAF+∠AFB=25°+95°=120°，
∴∠DAC=30°，∠BOA=120°．
故∠DAE=5°，∠BOA=120°．
【解析】先利用三角形内角和定理可求∠ABC，在直角三角形ACD中，易求∠DAC；再根据角平分线定义可求∠CBF、∠EAF，可得∠DAE的度数；然后利用三角形外角性质，可先求∠AFB，再次利用三角形外角性质，容易求出∠BOA．
口算与应用题卡系列答案
名师点睛字词句段篇系列答案科目：初中数学 来源： 题型：
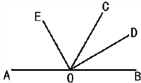
【题目】如图，点O在直线AB上，OE、OD分别是∠AOC、∠BOC的平分线.
(1)∠AOE的补角是∠____；∠BOD的余角是______；
(2)若∠AOC=118°，求∠COD的度数；
(3)射线OD与OE之间有什么特殊的位置关系？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知代数式
，当
时，该代数式的值为-1.
（1）求
的值。
（2）已知当
时，该代数式的值为-1，求
的值。
（3）已知当
时，该代数式的值为9，试求当
时该代数式的值。
（4）在第（3）小题已知条件下，若有
成立，试比较
与
的大小。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)如图①，在△ABC中，点O是∠ABC和∠ACB的平分线的交点，若∠A＝α，则∠BOC＝90°＋
；如图②，∠CBO＝
∠ABC，∠BCO＝
∠ACB，∠A＝α，则∠BOC＝__________(用α表示)；
(2)如图③，∠CBO＝
∠DBC，∠BCO＝
∠ECB，∠A＝α，请猜想∠BOC＝__________(用α表示)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．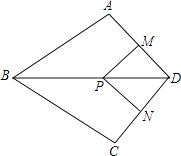 
（1）求证：∠ADB=∠CDB；
（2）若∠ADC=90°，求证：四边形MPND是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(12分)当我们利用两种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图①，可得等式：(a＋2b)(a＋b)＝a2＋3ab＋2b2.
(1)由图②，可得等式：__________________________；
(2)利用(1)中所得到的结论，解决下面的问题：
已知a＋b＋c＝11，ab＋bc＋ac＝38，求a2＋b2＋c2的值；
(3)利用图③中的纸片(足够多)，画出一种拼图，使该拼图可用来验证等式：2a2＋5ab＋2b2＝(2a＋b)(a＋2b);
(4)琪琪用2张边长为a的正方形，3张边长为b的正方形，5张边长分别为a，b的长方形纸片重新拼出一个长方形，那么该长方形较长的一条边长为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
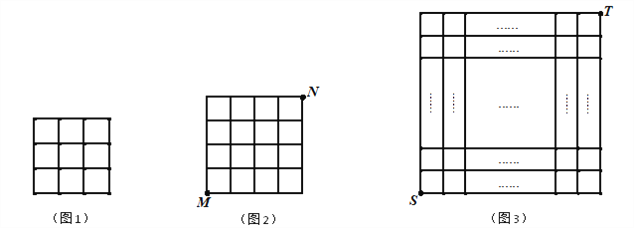
【题目】在每个小正方形的边长为1的网格中，每个小正方形的顶点称为格点．我们将从一个格点移动到与之相距
的另一个格点的运动称为一次跳马变换．
（1）在图1中画出边长为
的正方形，使它的顶点在网格的格点上．
（2）在图2中有一只电子小马从格点
出发，经过跳马变换到达与其相对的格点
，则最少需要跳马变换的次数是 次．
（3）如图3，在
的正方形网格中，一只电子小马从格点
经过若干次跳马变换到达与其相对的格点
，则它跳过的最短路程为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com