
【题目】如图,∠AOB=30°,点P是它内部一点,OP=2,如果点Q、点R分别是OA、OB上的两个动点,那么PQ+QR+RP的最小值是__________.

【答案】2
【解析】
先作点P关于OA,OB的对称点P′,P″,连接P′P″,由轴对称确定最短路线问题,P′P″分别与OA,OB的交点即为Q,R,△PQR周长的最小值=P′P″,由轴对称的性质,可证∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP=2, ∠P′OP″=2∠AOB=2×30°=60°,继而可得△OP′P″是等边三角形,即PP′=OP′=2.
作点P关于OA,OB的对称点P′,P″,连接P′P″,
由轴对称确定最短路线问题,P′P″分别与OA,OB的交点即为Q,R,
△PQR周长的最小值=P′P″,由轴对称的性质,
∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP=2,
所以,∠P′OP″=2∠AOB=2×30°=60°,
所以,△OP′P″是等边三角形,
所以,PP′=OP′=2.
故答案为:2.


科目:初中数学 来源: 题型:
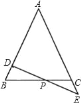
【题目】如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P.
(1)求证:PE=PD;
(2)若CE:AC=1:5,BC=10,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上从左到右的三个点![]() ,
,![]() ,
,![]() 所对应的数分别为
所对应的数分别为![]() ,
,![]() ,
,![]() .其中
.其中![]() ,
,![]() ,如图所示.
,如图所示.

(1)若以![]() 为原点,写出点
为原点,写出点![]() ,
,![]() 所对应的数,并计算
所对应的数,并计算![]() 的值.
的值.
(2)若原点![]() 在
在![]() ,
,![]() 两点之间,求
两点之间,求![]() 的值.
的值.
(3)若![]() 是原点,且
是原点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE.
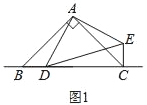
(1)在图1中,当点D在边BC上时,求证:BC=CE+CD;
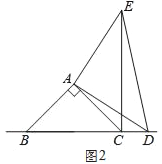
(2)在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;
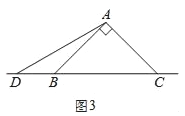
(3)在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题: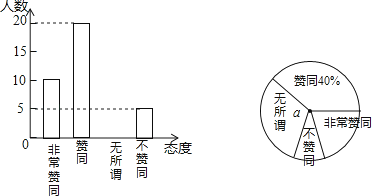
(1)在这次问卷调查中一共抽取了名学生,a=%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点 A,B 到表示2 的点的距离都为 9,P 为线段 AB 上任一点,C,D 两点分别从 P,B 同时向 A 点移动,且 C 点运动速度为每秒 3 个单位长度,D 点运动速度为每秒 4 个单位长度,运动 3 秒时,CD=4,则 P 点表示的数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为 1,宽为 a 的长方形纸片(0.5<a<1)如图折叠,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图折叠,剪下一个边长等于此时长方形宽度的正方形 (称为第二次操作);如此反复操作下去,如此反复下去,若在第 n 次操作后剩下的长方形恰好为正方形,则操作终止.

(1)第一次操作后,剩下的长方形两边长分别为 ;(用含 a 的代数式表示)
(2)若第二次操作后,剩下的长方形恰好是正方形,则求 a 的值,写出解答过程;
(3)若第三次操作后,剩下的长方形恰好是正方形,画出示意图形,直接写出 a 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由组成的图案和算式,解答问题:
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算 1+3+5+7+9+11;
(2)请计算 1+3+5+7+9+…+19;
(3)请计算 1+3+5+7+9+…+(2n﹣1);
(4)请用上述规律计算:21+23+25+…+99.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com