
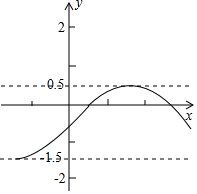 对于某一函数,给出如下定义:若存在实数M>0,对于一函数任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的确界值.例如如图所示的函数是有界函数,其确界值是1.5.问:将函数y=-x2(-m≤x≤1,m≥o)的图象向上平移m个单位,得到的函数的确界值是t,当m在什么范围时,满足$\frac{3}{4}≤t≤1$.
对于某一函数,给出如下定义:若存在实数M>0,对于一函数任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的确界值.例如如图所示的函数是有界函数,其确界值是1.5.问:将函数y=-x2(-m≤x≤1,m≥o)的图象向上平移m个单位,得到的函数的确界值是t,当m在什么范围时,满足$\frac{3}{4}≤t≤1$. 分析 需要分类讨论:m>1和m≤1两种情况.函数向上平移m个单位后,分别求出此时确界值,再判断题意是否相符,得到结论即可.
解答 解:(1)若m>1时,函数y=-x2向上平移m个单位后,当时函数的值大于 1,显然与题意不符.
只能m≤1;
(2)∵m≤1,
∴右端点离对称轴近不可能是最值,最大值只能的顶点,最小值只能是左端点.
∵对于函数y=-x2
当x=0时,y man=0
当x=-1时,ymin=-1
∴相应的对于函数y=-x2+m
当x=0时,y man=m
当x=-1时,ymin=-1+m(5分)
∴需 最大在$\frac{3}{4}$与1之间 或 最小在-1与$-\frac{3}{4}$之间
$\frac{3}{4}$≤m≤1 或 $-1≤-1+m≤-\frac{3}{4}$
∴$\frac{3}{4}≤m≤1$或$0≤m≤\frac{1}{4}$.
点评 本题考查了二次函数综合题,结合新定义,弄清函数边界值的定义,同时要熟悉平移变换的性质.


科目:初中数学 来源: 题型:填空题
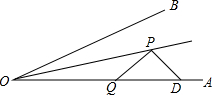 如图:已知∠AOB=30°,D是OA上一点,且OD=6cm,射线OC平分∠AOB,P、Q分别是射线OC、线段OA上的动点,则PQ+PD的最小值=3.
如图:已知∠AOB=30°,D是OA上一点,且OD=6cm,射线OC平分∠AOB,P、Q分别是射线OC、线段OA上的动点,则PQ+PD的最小值=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com