
| 老师在课堂上放手让学生提问和表达情况调查 | |||||
| 选项 | A | B | C | D | E |
| 内容 | 从不 | 很少 | 有时 | 常常 | 总是 |
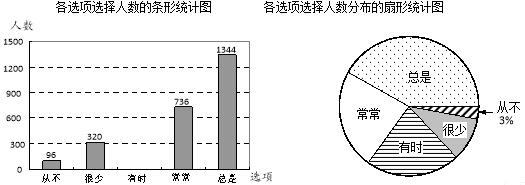
分析 (1)由扇形统计图和条形统计图可知,选择从不的有96人占3%,从而可以得到该区参加了本次问卷调查的八年级的学生共有多少名;
(2)根据题意可以算出选择有时的人数,从而可以将条形统计图补充完整;
(3)根据统计图可以求得在扇形统计图中,“总是”所占的百分比.
解答 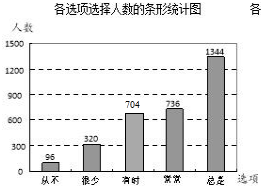 解:(1)由题意可得,
解:(1)由题意可得,
96÷3%=3200(名),
即该区参加了本次问卷调查的八年级的学生共有多少名该区参加了本次问卷调查的八年级的学生共有3200名;
(2)由题意可得,
参与调查的选择有时的人数有:3200-96-320-736-1344=704,
补全的条形统计图如右图所示,
(3)由题意可得,
在扇形统计图中,“总是”所占的百分比是:1344÷3200×100%=42%,
即在扇形统计图中,“总是”所占的百分比是42%.
点评 本题考查条形统计图、扇形统计图,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:选择题
| A. | m+n | B. | n-m | C. | m-n | D. | -m-n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四个角相等的四边形是矩形 | |
| B. | 四边相等的四边形是正方形 | |
| C. | 对角线相等的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com