
【题目】如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
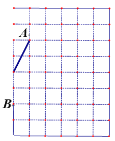
(1)在方格纸中画出以∠ABC为直角的直角三角形ABC,点C在小正方形的顶点上,且三角形ABC的面积为5;
(2)在方格纸中画出以AB为一边的菱形ABDE,点D、E在小正方形的顶点上,且菱形ABDE的面积为3,连接CE,请直接写出线段CE的长.
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】只利用一把有刻度的直尺,用度量的方法按下列要求画图:
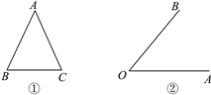
(1)在图①中用下面的方法画等腰三角形ABC的对称轴.
①量出底边BC的长度,将线段BC二等分,即画出BC的中点D;
②画直线AD,即画出等腰三角形ABC的对称轴.
(2)在图②中画∠AOB的对称轴,并写出画图的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
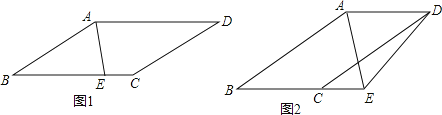
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.
①求证∠ABC=∠ADC;
②求∠CED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为____________海里/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
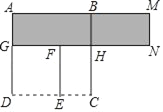
【题目】如图,四边形ABCD与四边形DEFG都是正方形,设AB=a,DE=b(a>b).
(1)写出AG的长度(用含字母a,b的代数式表示);
(2)观察图形,当用不同的方法表示图形中阴影部分的面积时,你能获得一个因式分解公式,请将这个公式写出来;
(3)如果正方形ABCD的边长比正方形DEFG的边长多16cm,它们的面积相差960cm2,试利用(2)中的公式,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com