练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．如图，在△ABC中，AC=BC，分别以点A、C为圆心，大于$\frac{1}{2}$AC的长为半径作弧相交于点M、N，作直线MN，分别交AC、BC于点D、E，连结AE，若△AEB的周长是10，则AB+BC=10．

    分析 根据尺规作图得到DE是线段AC的垂直平分线，根据线段垂直平分线的性质得到EA=EC，根据三角形周长公式计算即可．

    解答 解：由尺规作图可知，DE是线段AC的垂直平分线，
    ∴EA=EC，
    ∵△AEB的周长是10，
    ∴AE+AB+BE=10，
    ∴AB+BE+EC=10，
    ∴AB+BC=10，
    故答案为：10．

    点评 本题考查的是基本尺规作图和线段垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．按学校规划要求，现要将校园区域内的一块用篱笆围成的直径为50m的圆形植物园改建成长方形的形状，使得它的长比宽多5m，并恰好能用原来的篱笆围起来．请问：长方形的长和宽各是多少？（结果精确到0.1m）？试比较改建后的植物园的面积与原来的面积有何变化？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．把△ABC三条边的长度都扩大2倍，则锐角A的三角函数值（　　）
    A．也扩大2倍B．缩小为原来的$\frac{1}{2}$C．都不变D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．探究问题
    （1）阅读操作，在小学阶段我们学过，任何有限位小数都可以转化成分数的形式．
    请你将下列各数化成分数形式：
    ①-3.14=-$\frac{157}{50}$ ②-5.6=-$\frac{28}{5}$
    （2）发现问题，我们小学阶段的小数，除有限位小数外，还有无限位的小数，那就是无限循环小数．
    （3）提出问题，对于无限循环小数如何将其化成分数的形式？
    （4）分析问题：例如：如何将0.$\stackrel{•}{1}\stackrel{•}{4}$化成分数的形式？
    分析：假设x=0.$\stackrel{•}{1}\stackrel{•}{4}$，由等式的基本性质得，100x=14.$\stackrel{•}{1}\stackrel{•}{4}$，
    即100x=14+0.$\stackrel{•}{1}\stackrel{•}{4}$，也就是100x=14+x，
    解这个关于x的一元一次方程，得x=$\frac{14}{99}$，所以0.$\stackrel{•}{1}\stackrel{•}{4}$=$\frac{14}{99}$
    说明可以将0.$\stackrel{•}{1}\stackrel{•}{4}$化成分数的形式．
    （5）解决问题．请你类比上面的做法，将下列的无限循环小数化成整数或分数的形式：
    ①0.$\stackrel{•}{9}$=1，②-0.$\stackrel{•}{1}\stackrel{•}{0}$=-$\frac{10}{99}$，③2.$\stackrel{•}{4}0\stackrel{•}{5}$=2$\frac{405}{999}$
    （6）归纳结论：整数部分为0的无限循环小数=$\frac{小数部分}{9…（9的个数等于小数部分的数字个数）}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，阴影部分四边形的两个顶点依次在x轴上，其中横坐标分别为1、3、5的顶点A1、A2、A3在一次函数y=2x+5的图象上，横坐标分别为1、3、5的顶点B1、B2、B3在一次函数y=x+3的图象上，记第一个阴影部分四边形面积为S1，第二个阴影部分四边形面积为S2，第三个阴影部分面积为S3，…，则第2015个阴影部分四边形的面积是（　　）
    A．2015B．2017C．4029D．4031

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列对平移的描述正确的是（　　）
    A．坐在秋千上的人的运动是平移
    B．把一个20°的角向右平移2个单位后度数为40°
    C．水平线段AB=2cm，向上平移2个单位后得线段CD，则CD∥AB，且CD=2cm
    D．同一个人手心朝上的两只手，左手可以通过平移与右手重合

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．若代数式3a+2b-4的值为2，那么代数式9a+6b-11的值为（　　）
    A．29B．-17C．7D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．若y关于x的一次函数y=（m-2）x+m-3中，y随着x的增大而增大，且图象与y轴的交点在x轴下方，则m的取值范围是2＜m＜3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

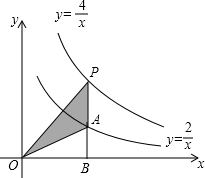    9．如图，点P是反比例函数y=$\frac{4}{x}$上任意一点，PB⊥x轴交反比例函数y=$\frac{2}{x}$于点A，则△POA的面积为1．

    查看答案和解析>>

    同步练习册答案