
дкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊM1ЃЈ3ЃЌ2ЃЉЃЌN1ЃЈ5ЃЌЉ1ЃЉЃЌЯпЖЮM1N1ЦНвЦжСЯпЖЮMNДІЃЈзЂЃКM1гыMЃЌN1гыNЗжБ№ЮЊЖдгІЕуЃЉЃЎ

ЃЈ1ЃЉШєMЃЈЉ2ЃЌ5ЃЉЃЌЧыжБНгаДГіNЕузјБъЃЎ
ЃЈ2ЃЉдкЃЈ1ЃЉЮЪЕФЬѕМўЯТЃЌЕуNдкХзЮяЯп ЩЯЃЌЧѓИУХзЮяЯпЖдгІЕФКЏЪ§НтЮіЪНЃЎ
ЩЯЃЌЧѓИУХзЮяЯпЖдгІЕФКЏЪ§НтЮіЪНЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЮЪЬѕМўЯТЃЌШєХзЮяЯпЖЅЕуЮЊBЃЌгыyжсНЛгкЕуAЃЌЕуEЮЊЯпЖЮABжаЕуЃЌЕуCЃЈ0ЃЌmЃЉЪЧyжсИКАыжсЩЯвЛЖЏЕуЃЌЯпЖЮECгыЯпЖЮBOЯрНЛгкFЃЌЧвOCЃКOF=2ЃК ЃЌЧѓmЕФжЕЃЎ
ЃЌЧѓmЕФжЕЃЎ
ЃЈ4ЃЉдкЃЈ3ЃЉЮЪЬѕМўЯТЃЌЖЏЕуPДгBЕуГіЗЂЃЌбиxжсе§ЗНЯђдШЫйдЫЖЏЃЌЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЈМДBPГЄЮЊЖрЩйЃЉЃЌНЋЁїABPбиБпPEелЕўЃЌЁїAPEгыЁїPBEжиЕўВПЗжЕФУцЛ§ЧЁКУЮЊДЫЪБЕФЁїABPУцЛ§ЕФ ЃЌЧѓДЫЪБBPЕФГЄЖШЃЎ
ЃЌЧѓДЫЪБBPЕФГЄЖШЃЎ
НтЃКЃЈ1ЃЉЃЈ0ЃЌ2ЃЉЁЃ
ЃЈ2ЃЉЁпNЃЈ0ЃЌ2ЃЉдкХзЮяЯп ЩЯЃЌЁрk=2ЁЃ
ЩЯЃЌЁрk=2ЁЃ

ЁрХзЮяЯпЕФНтЮіЪНЮЊ ЁЃ
ЁЃ
ЃЈ3ЃЉЁп ЃЌ
ЃЌ
ЁрBЃЈ ЃЌ0ЃЉЁЂAЃЈ0ЃЌ2ЃЉЁЂEЃЈ
ЃЌ0ЃЉЁЂAЃЈ0ЃЌ2ЃЉЁЂEЃЈ ЃЌ1ЃЉЁЃ
ЃЌ1ЃЉЁЃ
ЁпCOЃКOF=2ЃК ЃЌ
ЃЌ
ЁрCO=ЉmЃЌFO= mЃЌ
mЃЌ ЁЃ
ЁЃ
Ёп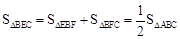 ЃЌЁр
ЃЌЁр ЁЃ
ЁЃ
ећРэЕУЃКm2+m=0ЁЃЁрm=Љ1Лђ0 ЁЃ
ЁпmЃМ0ЃЌЁрm=Љ1ЁЃ
ЃЈ4ЃЉдкRtЁїABOжаЃЌ ЃЌ
ЃЌ
ЁрЁЯABO=30ЁуЃЌAB=2AO=4
ЂйЕБЁЯBPEЃОЁЯAPEЪБЃЌСЌНгA1BЃЌдђЖделКѓШчЭМ2ЃЌA1ЮЊЖделКѓAЕФЫљТфЕуЃЌЁїEHPЪЧжиЕўВПЗжЁЃ

ЁпEЮЊABжаЕуЃЌЁрSЁїAEP=SЁїBEP= SЁїABPЁЃ
SЁїABPЁЃ
ЁпSЁїEHP= SЁїABPЃЌЁр
SЁїABPЃЌЁр =SЁїEHP=SЁїBHP=
=SЁїEHP=SЁїBHP= SЁїABPЁЃ
SЁїABPЁЃ
ЁрA1H=HPЃЌEH=HB=1ЁЃЁрЫФБпаЮA1BPEЮЊЦНааЫФБпаЮЁЃ
ЁрBP=A1E=AE=2ЁЃ
ЂкЕБЁЯBPE=ЁЯAPEЪБЃЌжиЕўВПЗжУцЛ§ЮЊЁїABPУцЛ§ЕФвЛАыЃЌВЛЗћКЯЬтвтЁЃ
ЂлЕБЁЯBPEЃМЁЯAPEЪБЃЎдђЖделКѓШчЭМ3ЃЌA1ЮЊЖделКѓAЕФЫљТфЕуЃЌЁїEHPЪЧжиЕўВПЗжЁЃ

ЁпEЮЊABжаЕуЃЌЁрSЁїAEP=SЁїBEP= SЁїABPЁЃ
SЁїABPЁЃ
ЁпSЁїEHP= SЁїABPЃЌЁрSЁїEBH=SЁїEHP=
SЁїABPЃЌЁрSЁїEBH=SЁїEHP= =
= SЁїABPЁЃ
SЁїABPЁЃ
ЁрBH=HPЃЌEH=HA1=1ЁЃ
гжЁпBE=EA=2ЃЌЁрEH
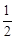 APЁЃЁрAP=2ЁЃ
APЁЃЁрAP=2ЁЃ
дкЁїAPBжаЃЌЁЯABP=30ЁуЃЌAB=4ЃЌAP=2ЃЌ
ЁрЁЯAPB=90ЁуЁЃЁрBP= ЁЃ
ЁЃ
злЩЯЫљЪіЃЌBP=2Лђ ЁЃ
ЁЃ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШИљОнЕуMЕФвЦЖЏЗНЯђКЭЕЅЮЛЕУЕНЕуNЕФЦНвЦЗНЯђКЭЕЅЮЛЃЌШЛКѓАДееЦНвЦЗНЯђКЭЕЅЮЛНјаавЦЖЏМДПЩЃК
гЩгкЭМаЮЦНвЦЙ§ГЬжаЃЌЖдгІЕуЕФЦНвЦЙцТЩЯрЭЌЃЌ
гЩЕуMЕНЕуMЁфПЩжЊЃЌЕуЕФКсзјБъМѕ5ЃЌзнзјБъМг3ЃЌ
ЙЪЕуNЁфЕФзјБъЮЊЃЈ5Љ5ЃЌЉ1+3ЃЉЃЌМДЃЈ0ЃЌ2ЃЉЁЃ
ЃЈ2ЃЉНЋЕуNЕФзјБъДњШыКЏЪ§ЕФНтЮіЪНМДПЩЧѓЕУkжЕЁЃ
ЃЈ3ЃЉХфЗНКѓШЗЖЈЕуBЁЂAЁЂEЕФзјБъЃЌИљОнCOЃКOF=2ЃК ЃЌгУmБэЪОГіЯпЖЮCOЁЂFOКЭBFЕФГЄЃЌРћгУ
ЃЌгУmБэЪОГіЯпЖЮCOЁЂFOКЭBFЕФГЄЃЌРћгУ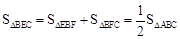 ЕУЕНЙигкmЕФЗНГЬЃЌЧѓЕУmЕФжЕМДПЩЁЃ
ЕУЕНЙигкmЕФЗНГЬЃЌЧѓЕУmЕФжЕМДПЩЁЃ
ЃЈ4ЃЉЗжЕБЁЯBPEЃМЁЯAPEЪБЁЂЕБЁЯBPE=ЁЯAPEЪБЁЂЕБЁЯBPEЃМЁЯAPEЪБШ§жжЧщПіЗжРрЬжТлМДПЩЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 зјБъдЕуЃЎAЁЂBСНЕуЕФКсзјБъЗжБ№ЪЧЗНГЬx2-4x-12=0ЕФСНИљЃЌЧвcosЁЯDAB=
зјБъдЕуЃЎAЁЂBСНЕуЕФКсзјБъЗжБ№ЪЧЗНГЬx2-4x-12=0ЕФСНИљЃЌЧвcosЁЯDAB=
| ||
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 18ЁЂдкЦНУцжБНЧзјБъЯЕжаЃЌАбвЛИіЭМаЮЯШШЦзХдЕуЫГЪБеыа§зЊЕФНЧЖШЮЊІШЃЌдйвддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊkЕУЕНвЛИіаТЕФЭМаЮЃЌЮвУЧАбетИіЙ§ГЬМЧЮЊЁОІШЃЌkЁПБфЛЛЃЎР§ШчЃЌАбЭМжаЕФЁїABCЯШШЦзХдЕуOЫГЪБеыа§зЊЕФНЧЖШЮЊ90ЁуЃЌдйвддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ2ЕУЕНвЛИіаТЕФЭМаЮЁїA1B1C1ЃЌПЩвдАбетИіЙ§ГЬМЧЮЊЁО90ЁуЃЌ2ЁПБфЛЛЃЎ
18ЁЂдкЦНУцжБНЧзјБъЯЕжаЃЌАбвЛИіЭМаЮЯШШЦзХдЕуЫГЪБеыа§зЊЕФНЧЖШЮЊІШЃЌдйвддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊkЕУЕНвЛИіаТЕФЭМаЮЃЌЮвУЧАбетИіЙ§ГЬМЧЮЊЁОІШЃЌkЁПБфЛЛЃЎР§ШчЃЌАбЭМжаЕФЁїABCЯШШЦзХдЕуOЫГЪБеыа§зЊЕФНЧЖШЮЊ90ЁуЃЌдйвддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ2ЕУЕНвЛИіаТЕФЭМаЮЁїA1B1C1ЃЌПЩвдАбетИіЙ§ГЬМЧЮЊЁО90ЁуЃЌ2ЁПБфЛЛЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com